【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数 ![]() 的图象抛物线经过A、C两点.
的图象抛物线经过A、C两点.

(1)求该二次函数的表达式;
(2)F,G分别为x轴、y轴上的动点,首尾顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否存在点P,使△ODP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)∵二次函数 ![]() 的图象经过A(0,4)、C(5,0)两点,
的图象经过A(0,4)、C(5,0)两点,
∴ ![]() 解得
解得 
∴二次函数的解析式为 ![]()
(2)∵四边形OABC为矩形,
∴∠BAO=∠AOC=90°,AB=OC=5,BC=OA=4,
∴B(5,4),
∵E为BC中点,
∴E(5,2),
∵OD平分∠AOC,
∴∠AOD=∠DOC=45°,
∴∠ADO=∠AOD=45°,
∴AD=OA=4,
∴D(4,4),
∴DE= ![]() ,
,
作D关于y轴的对称点D′,作E关于x轴的对称点E′,连接D′G、E′F,如下图所示:
则D′(-4,4),E′(5,-2),且D′G=DG,E′F=EF,
∵在 ![]() E′BD′中,∠E′BD′=90°,BD′=5-(-4)=9,E′B=4-(-2)=6,
E′BD′中,∠E′BD′=90°,BD′=5-(-4)=9,E′B=4-(-2)=6,
∴E′D′= ![]() ,
,
∵四边形DEFG的周长=DE+EF+FG+GD=DE+ E′F+FG+ GD′≥DE+ E′D′,
∴四边形DEFG的周长最小值为DE+ E′D′,
∴四边形DEFG周长的最小值是 ![]()
(3)解:∵点D的坐标是(4,4),
∴OD= ![]() ,
,
又∵使△ODP的面积为8,
∴点P到直线OD的距离为 ![]() ,
,
过点O作OF⊥OD,取OF= ![]() ,过点F作直线FG∥OD,交抛物线与点P1,P2,则,∠OFG=90°,如图所示:
,过点F作直线FG∥OD,交抛物线与点P1,P2,则,∠OFG=90°,如图所示:
∵∠DOC=45°(已求),
∴∠COF=∠FOG=45°,
在直角 ![]() 中,OF=
中,OF= ![]() ,
,
∴OG= ![]() =4,
=4,
∴直线GF的解析式为y=x-4,
把y=x-4代入 ![]() 中,得
中,得 ![]() ,
,
解得x1=4,x2=10,
把x1=4,x2=10代入y=x-4中,得y1=0,y2=6,
∴P1(4,0),P2(10,6),
过点O作OF⊥OD,取OF= ![]() ,过点F作直线FG交抛物线与P3,P4,如下图所示:
,过点F作直线FG交抛物线与P3,P4,如下图所示:
∵∠DOC=45°(已求),
∴∠DOA=∠AOF=∠GOF=45°,
在直角 ![]() 中,OF=
中,OF= ![]() ,
,
∴OG= ![]() =4,
=4,
∴直线GF的解析式为y=x+4,
把y=x+4代入 ![]() 中,得
中,得 ![]() ,
,
解得x1=0,x2=14,
把x1=0,x2=14代入y=x+4中,得y1=4,y2=18,
∴P1(0,4),P2(14,18),
所以综合上述可得,P1(4,0) 、 P2(10,6) 、P3(0,4) 、 P4(14,18)
【解析】(1)把A、C坐标代入解析式,解方程组,即可求出解析式;(2)利用对称法,做出D关于y轴的对称点D′,作E关于x轴的对称点E′,当D'、E'、F、G四点共线时,周长最小;(3)以OD为底边,使△ODP的面积为8,则点P到直线OD的距离为 2 ![]() ,在OD两侧作平行于OD的直线,使直线与直线OD的距离为 2
,在OD两侧作平行于OD的直线,使直线与直线OD的距离为 2 ![]() ,与抛物线交于4个点,解方程组,求出坐标.
,与抛物线交于4个点,解方程组,求出坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ABCD 中,∠A=160°,∠B=50°,∠ADC、∠BCD 的平分线相交于点E,则∠CED=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】[数学实验探索活动]
实验材料现有若干块如图①所示的正方形和长方形硬纸片.
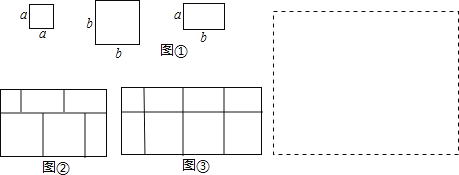
实验目的:
用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,得到相应的等式,从而探求出多项式乘法或分解因式的新途径.
例如,选取正方形、长方形硬纸片共 6 块,拼出一个如图②的长方形,计算它的面积, 写出相应的等式有 a2+3ab+2b2=(a+2b)(a+b)或 (a+2b)(a+b) =a2+3ab+2b2.
问题探索:
(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ,那么需要两种正方形纸片 张,长方形纸片 张;
(2)选取正方形、长方形硬纸片共 8 块,可以拼出一个如图③的长方形,计算图③的面积,并写出相应的等式;
(3)试借助拼图的方法,把二次三项式 2a2+5ab+2b2 分解因式,并把所拼的图形画在虚线方框内.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与应用:
阅读1:a、b为实数,且a>0,b>0,因为 ,所以
,所以  ,从而
,从而  (当a=b时取等号).
(当a=b时取等号).
阅读2:函数 (常数m>0,x>0),由阅读1结论可知:
(常数m>0,x>0),由阅读1结论可知: 
 ,所以当
,所以当  即
即  时,函数
时,函数  的最小值为
的最小值为  .
.
阅读理解上述内容,解答下列问题:
(1)问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ,周长为
,周长为  ,求当x=时,周长的最小值为 .
,求当x=时,周长的最小值为 .
(2)问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=时, 的最小值为 .
的最小值为 .
(3)问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数) -
科目: 来源: 题型:
查看答案和解析>>【题目】为提高农民收入,某区一水果公园引进一种新型蟠桃,蟠桃进价为每公斤40元.上市后通过一段时间的试营销发现:当蟠桃销售单价在每公斤40元至90元之间(含40元和90元)时,每月的销售量
 (公斤)与销售单价
(公斤)与销售单价 (元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.
(元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.(1)求
 与
与 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;(2)如果想要每月获得2400元的利润,那么销售单价应定为每公斤多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像与反比例函数
的图像与反比例函数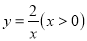 的图像相交于点
的图像相交于点 ,一次函数
,一次函数 与
与 轴相交于点
轴相交于点 ,与
,与 轴相交于点
轴相交于点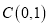 .
.(1)求
 和
和 的值;
的值;(2)点
 在
在 轴正半轴上,且
轴正半轴上,且 的面积为1,求点
的面积为1,求点 坐标;
坐标;(3)在(2)的条件下,点
 是一次函数
是一次函数 上一点,点
上一点,点 是反比例函数
是反比例函数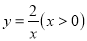 图像上一点,且点
图像上一点,且点 、
、 都在
都在 轴上方.如果以
轴上方.如果以 、
、 、
、 、
、 为顶点的四边形为平行四边形,请直接写出点
为顶点的四边形为平行四边形,请直接写出点 、
、 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,要使四边形ABCD是正方形,则需要添加一个条件是 . (填一个即可)

相关试题

