【题目】将正整数按如下图所示的规律排列,若用有序数对(m , n)表示从上到下第m行,和该行从左到右第n个数,如(4,2)表示整数8,则(8,4)表示的整数是( )
A.31
B.32
C.33
D.41
参考答案:
【答案】B
【解析】根据(4,2)表示整数8,是以连续自然数的形式排列,对图中给出的有序数对进行分析,可以发现:第1行1个数到最后一个数为1,第2行2个数最后一个数为1+2=3,第3行3个数最后一个数为1+2+3=6,……第7行最后一个数为1+2+3+4+5+6+7=28,而(8,4)表示第8行第四个数,所以第8行第四个数为28+4=32.
【考点精析】利用数与式的规律和坐标确定位置对题目进行判断即可得到答案,需要熟知先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律;对于平面内任一点P,过P分别向x轴,y轴作垂线,垂足分别在x轴,y轴上,对应的数a,b分别叫点P的横坐标和纵坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,我们曾经研究过
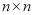 的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道:
的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道: 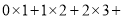 …
…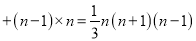 时,我们可以这样做:
时,我们可以这样做:(1)观察并猜想:
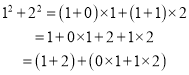 ;
; 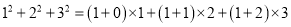
=
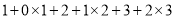
=
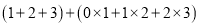 ;
;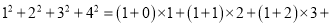
=
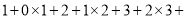
=
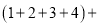 ( );…
( );…(2)归纳结论:
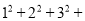 …
…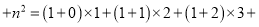 …
…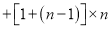
=
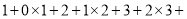 …
…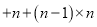
=( )+[ ]
= +
=
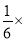 .
.(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在9×7的小正方形网格中,△ABC的顶点A,B,C在网格的格点上.将△ABC向左平移3个单位、再向上平移3个单位得到△A′B′C′.再将△ABC按一定规律依次旋转:第1次,将△ABC绕点B顺时针旋转
 得到△
得到△ ;第2次,将△
;第2次,将△ 绕点
绕点 顺时针旋转
顺时针旋转 得到△
得到△ ;第3次,将△
;第3次,将△ 绕点
绕点 顺时针旋转
顺时针旋转 得到△
得到△ ;第4次,将△
;第4次,将△ 绕点
绕点 顺时针旋转
顺时针旋转 得到△
得到△ 依次旋转下去.
依次旋转下去.
(1)在网格中画出△A′B′C′和△
 ;
;(2)请直接写出至少在第几次旋转后所得的三角形刚好为△A′B′C′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下利事件中,是随机事件的是( )
A.通常温度降到0℃以下,纯净的水结冰
B.明天太阳从东边升起
C.购买一张彩票,中奖
D.任意画一个三角形,其内角和为360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E , 交BC的延长线于点F .

(1)求证:BF=CD;
(2)连接BE , 若BE⊥AF , ∠F=60°,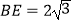 ,求
,求 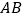 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):

请根据以上信息解答下列问题:
(1)表中的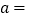 ,
, 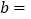 ;
;
(2)在图中补全频数分布直方图;
(3)若视力在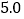 以上(含
以上(含 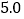 )均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有人.
)均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有人. -
科目: 来源: 题型:
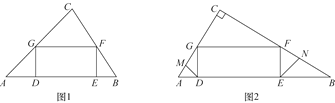
查看答案和解析>>【题目】在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F,G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若
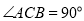 ,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF; (3)求出矩形DEFG的面积的最大值.
相关试题

