【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
参考答案:
【答案】(1)第一批悠悠球每套的进价是25元;(2)每套悠悠球的售价至少是35元.
【解析】
(1)设第一批悠悠球每套的进价是x元,则第二批悠悠球每套的进价是(x+5)元,根据数量=总价÷单价结合第二批购进数量是第一批数量的1.5倍,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设每套悠悠球的售价为y元,根据销售收入-成本=利润结合全部售完后总利润不低于25%,即可得出关于y的一元一次不等式,解之取其中的最小值即可得出结论.
(1)设第一批悠悠球每套的进价是x元,则第二批悠悠球每套的进价是(x+5)元,
根据题意得:
![]() ,
,
解得:x=25,
经检验,x=25是原分式方程的解.
答:第一批悠悠球每套的进价是25元.
(2)设每套悠悠球的售价为y元,
根据题意得:500÷25×(1+1.5)y-500-900≥(500+900)×25%,
解得:y≥35.
答:每套悠悠球的售价至少是35元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
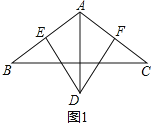
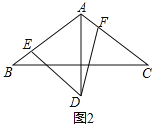
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2 , 若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的分式方程
 .
.(1)若方程的增根为x=2,求a的值;
(2)若方程有增根,求a的值;
(3)若方程无解,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(提示:正方形的四条边都相等,四个角都是直角)
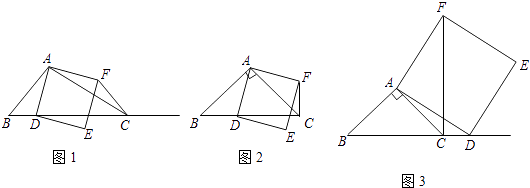
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF,BD所在直线的位置关系为 , 线段CF,BD的数量关系为;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足条件时,CF⊥BC(点C,F不重合),不用说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)
 ;(2)
;(2) ;(3)
;(3) +1=
+1=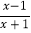 .
.
相关试题

