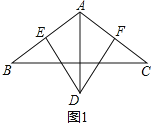
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
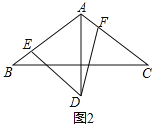
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
参考答案:
【答案】(1)见解析;![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接BD,证△ABD是等边三角形,得∠ABD=∠BDA=∠DAB=60,再证△BDE≌△ADF(AAS),AF=BE,故AB=AE+BE;
(2)线段AE,AF,AD之间的数量关系为:![]() ,思路如下:
,思路如下:
连接BD,模仿(1)证△BDE≌△ADF(AAS),得![]() ,所以
,所以![]() .
.
∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120
∴∠BAD=∠FAD=60
∵AD=AB
∴△ABD是等边三角形
∴∠ABD=∠BDA=∠DAB=60
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFA=90
在△BDE和△ADF中,
∠BED=∠DFA,∠EBD=∠FAD,BD=DA,
∴△BDE≌△ADF(AAS)
∴AF=BE
∴AB=AE+BE
∴AB=AE+AF
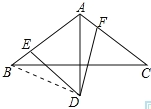
![]() 解:线段AE,AF,AD之间的数量关系为:
解:线段AE,AF,AD之间的数量关系为:![]() ,理由如下:
,理由如下:
连接BD,如图所示:
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,
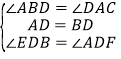 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
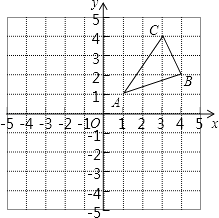
(1)①请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=30度.
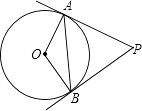
(1)求∠APB的度数;
(2)当OA=3时,求AP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
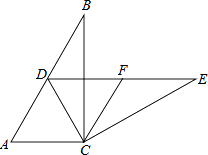
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2 , 若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的分式方程
 .
.(1)若方程的增根为x=2,求a的值;
(2)若方程有增根,求a的值;
(3)若方程无解,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
相关试题

