【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

参考答案:
【答案】(1)MN=AM+BN成立,理由见解析;(2)MN=BNAM,理由见解析.
【解析】
(1)利用同角的余角相等证明∠MAC=∠NCB,由∠AMC=∠CNB=90°,AC=BC,可证△AMC≌△CNB,从而有AM=CN,MC=BN,即可得出结论;
(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系.
解:(1)MN=AM+BN成立;
理由:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,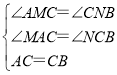 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=BN,
∵MN=CN+MC,
∴MN=AM+BN;
(2)MN=BNAM.
理由:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,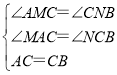 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=BN,
∵MN=MCCN,
∴MN=BNAM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有( )对.

A. 2B. 3C. 4D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间的距离吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为_______.
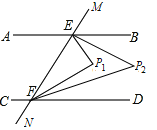
-
科目: 来源: 题型:
查看答案和解析>>【题目】“小口罩,大温暖”为有效防控疫情,缓解基层防疫物资短缺问题,2020年2月10日,福山区首批4万只口罩免费派发.烟台市政府紧急调拨的这批民用口罩包括A,B两种不同款型,其中A型口罩单价80元/盒,B型口罩单价100元/盒.
(1)先进行试点发放,某社区环卫工人共收到A、B两种款型的口罩100盒,总价值共计9200元.求免费发放给该社区环卫工人的A型口罩和B型口罩各多少盒?
(2)我区某街道办事处决定将此项公益活动在其整个街道社区全面铺开.此公益活动得到部分厂家支持,某口罩制造厂对此批口罩进行打折销售,具体如下:A型口罩按原价的八折销售,B型口罩超出5盒的的部分按原价的六折销售.分别写出购买两种口罩费用y关于购买数量x(x>5)的函数关系式;并求购买多少盒口罩时,两种型号口罩花费同样多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
 ,
, 、
、 分别是
分别是 和
和 上的动点,点
上的动点,点 为直线
为直线 、
、 之间任一点,且
之间任一点,且 ,则
,则 与
与 之间的数量关系为______.
之间的数量关系为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线
 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线
 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.

相关试题

