【题目】如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间的距离吗?
参考答案:
【答案】见解析
【解析】
试题(1)过点B作AB的垂线BF,在BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可证△EDC≌△ABC,即可证明DE=BA;
(2)从点B出发沿湖岸画一条射线BF,在BF上截取BC=CD,过点D作DE∥AB,使A、C、E在同一直线上,这时△EDC≌△ABC,则DE=AB.即DE的长就是A、B间的距离.
要测量A、B间的距离,可用如下方法:
(1)过点B作AB的垂线BF,在BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,根据“角边角公理”可知:△EDC≌△ABC.因此:DE=AB.即测出DE的长就是A、B之间的距离.(如图)

(2)从点B出发沿湖岸画一条射线BF,在BF上截取BC=CD,过点D作DE∥AB,使A、C、E在同一直线上,这时△EDC≌△ABC,则DE=AB.即DE的长就是A、B间的距离.(如图)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若∠B=30°,AB=8,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3
 的值;
的值;(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有( )对.

A. 2B. 3C. 4D. 1
-
科目: 来源: 题型:
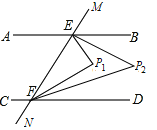
查看答案和解析>>【题目】如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“小口罩,大温暖”为有效防控疫情,缓解基层防疫物资短缺问题,2020年2月10日,福山区首批4万只口罩免费派发.烟台市政府紧急调拨的这批民用口罩包括A,B两种不同款型,其中A型口罩单价80元/盒,B型口罩单价100元/盒.
(1)先进行试点发放,某社区环卫工人共收到A、B两种款型的口罩100盒,总价值共计9200元.求免费发放给该社区环卫工人的A型口罩和B型口罩各多少盒?
(2)我区某街道办事处决定将此项公益活动在其整个街道社区全面铺开.此公益活动得到部分厂家支持,某口罩制造厂对此批口罩进行打折销售,具体如下:A型口罩按原价的八折销售,B型口罩超出5盒的的部分按原价的六折销售.分别写出购买两种口罩费用y关于购买数量x(x>5)的函数关系式;并求购买多少盒口罩时,两种型号口罩花费同样多?
相关试题

