【题目】已知,直线![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,点
上的动点,点![]() 为直线
为直线![]() 、
、![]() 之间任一点,且
之间任一点,且![]() ,则
,则![]() 与
与![]() 之间的数量关系为______.
之间的数量关系为______.
参考答案:
【答案】![]() 或
或![]()
【解析】
分两种情况进行讨论:①过点P作PQ∥AB,根据平行公理可得PQ∥CD,再根据两直线平行,内错角相等可得∠AMP=∠1,∠CNP=∠2,然后根据∠P=∠1+∠2等量代换即可得解;②过点P作PQ∥AB,根据平行公理可得PQ∥CD,再根据两直线平行,同旁内角互补可得∠AMP=180°-∠1,∠CNP=180°-∠2,然后根据∠P=∠1+∠2等量代换即可得解.
解:分两种情况: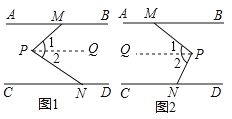
如图1,过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=∠1,∠CNP=∠2,
∵PM⊥PN,
∴∠MPN=∠1+∠2=90°,
∴∠AMP+∠CNP=90°;
如图2,过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=180°-∠1,∠CNP=180°-∠2,
∴∠AMP+∠CNP=180°×2-∠1-∠2,
∵∠MPN=∠1+∠2=90°,
∴∠AMP+∠CNP=360°-90°=270°;
综上所述,∠AMP与∠CNP之间的数量关系为:∠AMP+∠CNP=90°或∠AMP+∠CNP=270°.
故答案为:∠AMP+∠CNP=90°或∠AMP+∠CNP=270°.
-
科目: 来源: 题型:
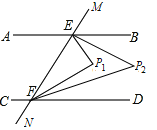
查看答案和解析>>【题目】如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“小口罩,大温暖”为有效防控疫情,缓解基层防疫物资短缺问题,2020年2月10日,福山区首批4万只口罩免费派发.烟台市政府紧急调拨的这批民用口罩包括A,B两种不同款型,其中A型口罩单价80元/盒,B型口罩单价100元/盒.
(1)先进行试点发放,某社区环卫工人共收到A、B两种款型的口罩100盒,总价值共计9200元.求免费发放给该社区环卫工人的A型口罩和B型口罩各多少盒?
(2)我区某街道办事处决定将此项公益活动在其整个街道社区全面铺开.此公益活动得到部分厂家支持,某口罩制造厂对此批口罩进行打折销售,具体如下:A型口罩按原价的八折销售,B型口罩超出5盒的的部分按原价的六折销售.分别写出购买两种口罩费用y关于购买数量x(x>5)的函数关系式;并求购买多少盒口罩时,两种型号口罩花费同样多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线
 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线
 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
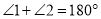 ,
, ,
, ,求
,求 的度数.(请填空完成下面的解答,其中括号内填说理的依据)
的度数.(请填空完成下面的解答,其中括号内填说理的依据)解:因为
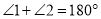
所以 (同旁内角互补,两直线平行)
所以
 又因为
又因为 ,所以 (等量代换)
,所以 (等量代换)所以
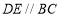 所以
所以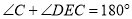 又因为
又因为
所以
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 吨,a= .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?

相关试题

