【题目】如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线![]() 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线![]() 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.

参考答案:
【答案】(1)C(0,2);(2)![]() ;(3)y=
;(3)y=![]() x.
x.
【解析】试题分析:(1)根据题意可知点A,B的坐标分别为(2,0),(6,0),代入函数解析式即可求得抛物线的解析式,即可得点C的坐标;
(2)根据图象可得PQ+PB的最小值即是AQ的长,所以抛物线对称轴l是x=4.所以Q(8,m)抛物线上,∴m=2.过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,求的AQ的值即可;
(3)此题首先要证得OE∥CM,利用待定系数法求得CM的解析式,即可求得OE的解析式.
试题解析:(1)由已知,得A(2,0),B(6,0),
∵抛物线y=![]() x2+bx+c过点A和B,
x2+bx+c过点A和B,
则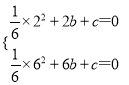
解得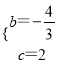
则抛物线的解析式为y=![]() x2-
x2-![]() x+2.
x+2.
故C(0,2).
(说明:抛物线的大致图象要过点A、B、C,其开口方向、顶点和对称轴相对准确)
(2)如图①,
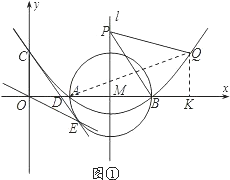
抛物线对称轴l是x=4.
∵Q(8,m)在抛物线上,
∴m=2.过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,
∴AQ=![]() .
.
又∵B(6,0)与A(2,0)关于对称轴l对称,
∴PQ+PB的最小值=AQ=2![]() .
.
(3)如图②,连接EM和CM.
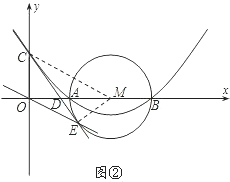
由已知,得EM=OC=2.
∵CE是⊙M的切线,
∴∠DEM=90°,
则∠DEM=∠DOC.
又∵∠ODC=∠EDM.
故△DEM≌△DOC.
∴OD=DE,CD=MD.
又在△ODE和△MDC中,∠ODE=∠MDC,∠DOE=∠DEO=∠DCM=∠DMC.
则OE∥CM.
设CM所在直线的解析式为y=kx+b,CM过点C(0,2),M(4,0),
∴![]()
解得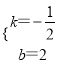
直线CM的解析式为y=![]() x+2.
x+2.
又∵直线OE过原点O,且OE∥CM,
∴OE的解析式为y=![]() x或y=0.5x.
x或y=0.5x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=﹣4,xy=2,则x2+y2的值( )
A. 10 B. 11 C. 12 D. 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x、y是有理数,设N=3x2+2y2﹣18x+8y+35,则N( )
A. 一定是负数 B. 一定不是负数 C. 一定是正数 D. N的取值与x、y的取值有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.

(1)若∠B=70°,求弧CD的度数;
(2)若AB=26,DE=8,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(4,0).点P是直线y=

 x+3在第一象限内的点,过P作PM
x+3在第一象限内的点,过P作PM x轴于点M,O是原点.
x轴于点M,O是原点. (1)设点P的坐标为(x, y),试用它的纵坐标y表示△OPA的面积S;
(2)S与y是怎样的函数关系?它的自变量y的取值范围是什么?
(3)如果用P的坐标表示△OPA的面积S,S与x是怎样的函数关系?它的自变量的取值范围是什么?
(4)在直线y=

 x+3上求一点Q,使△QOA是以OA为底的等腰三角形.
x+3上求一点Q,使△QOA是以OA为底的等腰三角形.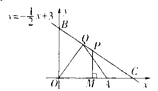
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:
 交y轴于点A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).(1)直线AB的表达式为______;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,直接写出点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左边到右边的变形,因式分解正确的是( )
A. 2a2﹣2=2(a+1)(a﹣1) B. (a+3)(a﹣3)=a2﹣9
C. ﹣ab2+2ab﹣3b=﹣b(ab﹣2a﹣3) D. x2﹣2x﹣3=x(x﹣2)﹣3
相关试题

