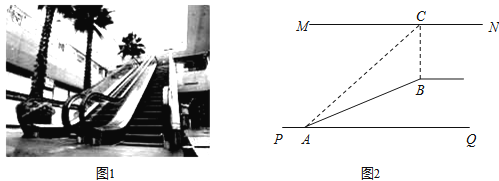
【题目】如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
参考答案:
【答案】BC约为2.5米.
【解析】
试题分析:延长CB交PQ于点D,根据坡度角的度数求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.
试题解析:延长CB交PQ于点D,

∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵坡角∠BAQ为37°,
∴![]() ≈0.75=
≈0.75=![]() ,
,
设BD=3x米,AD=4x米,则AB=5x米.
∵AB=12.5米,
∴x=2.5,
∴BD=7.5米,AD=10米.
在Rt△CDA中,∠CDA=90゜,∠CAQ=45°,
∴CD=AD=10米,
∴BC=CD-BD=10-7.5=2.5(米).
答:二楼的层高BC约为2.5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级640名学生在“计算机应用”培训前、后各参加了一次水平相同的测试,并以同一标准分成“不合格”、“合格”、“优秀”3个等级,为了解培训效果,用抽样调查的方式从中抽取32名学生的2次测试等级,并绘制成条形统计图:

(1)这32名学生经过培训,测试等级“不合格”的百分比比培训前减少了多少?
(2)估计该校八年级学生中,培训前、后等级为“合格”与“优秀”的学生各有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个一元一次方程的一次项系数与常数项的差刚好是这个方程的解,则称这个方程为妙解方程.例如:方程
 中,
中, ,方程的解为
,方程的解为 ,则方程
,则方程 为妙解方程.请根据上述定义解答下列问题:
为妙解方程.请根据上述定义解答下列问题:(1)方程
 是妙解方程吗?试说明理由.
是妙解方程吗?试说明理由.(2)已知关于
 的一元一次方程
的一元一次方程 是妙解方程.求
是妙解方程.求 的值.
的值.(3)已知关于
 的一元一次方程
的一元一次方程 是妙解方程,并且它的解是
是妙解方程,并且它的解是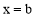 .求代数式
.求代数式 的值.
的值. -
科目: 来源: 题型:
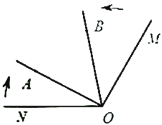
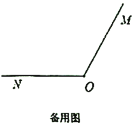
查看答案和解析>>【题目】如图,已知
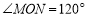 ,射线
,射线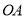 从
从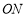 的位置开始绕点
的位置开始绕点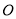 按顺时针方向旋转,速度是每秒
按顺时针方向旋转,速度是每秒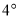 ,同时射线
,同时射线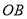 从
从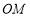 的位置开始绕点
的位置开始绕点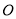 按逆时针方向旋转,速度是每秒
按逆时针方向旋转,速度是每秒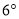 ,设旋转时间为
,设旋转时间为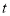 秒
秒 .
.
(1)用含
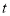 的代数式表示
的代数式表示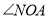 和
和 的度数;
的度数;(2)在旋转过程中,当
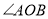 等于
等于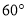 时,求
时,求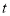 的值;
的值;(3)在旋转过程中是否存在这样的
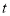 ,使得射线
,使得射线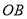 恰好是图中某个角的平分线?如果存在,请求出
恰好是图中某个角的平分线?如果存在,请求出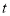 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.
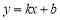 一定是一次函数
一定是一次函数B. 有的实数在数轴上找不到对应的点
C. 长为
 的三条线段能组成直角三角形
的三条线段能组成直角三角形D. 无论
 为何值,点
为何值,点 总是在第二象限
总是在第二象限 -
科目: 来源: 题型:
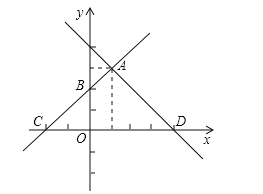
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,直线AB:y=k1x+b1与直线AD:y=k2x+b2相交于点A(1,3),且点B坐标为(0,2),直线AB交x轴负半轴于点C,直线AD交x轴正半轴于点D.
(1)求直线AB的函数解析式;
(2)若△ACD的面积为9,解不等式:k2x+b2>0;
(3)若点M为x轴一动点,当点M在什么位置时,使AM+BM的值最小?求出此时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地相距20
两地相距20 ,甲乙两人沿同一条路线从
,甲乙两人沿同一条路线从 地到
地到 地,如图的图象反映的是二人行进路程
地,如图的图象反映的是二人行进路程 (
( )与行进时间
)与行进时间 (
( )之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
)之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
A. 1个B. 2个C. 3个D. 4个
相关试题

