【题目】某校八年级640名学生在“计算机应用”培训前、后各参加了一次水平相同的测试,并以同一标准分成“不合格”、“合格”、“优秀”3个等级,为了解培训效果,用抽样调查的方式从中抽取32名学生的2次测试等级,并绘制成条形统计图:

(1)这32名学生经过培训,测试等级“不合格”的百分比比培训前减少了多少?
(2)估计该校八年级学生中,培训前、后等级为“合格”与“优秀”的学生各有多少名?
参考答案:
【答案】(1)50%;(2)140名、20名;320名、160名.
【解析】分析:(1)根据百分比的求法,用符合条件的人数除以总人数即可求出;
(2)分别根据抽样调查的百分比,估算出总的人数即可.
详解:(1)![]()
![]()
75%-25%=50%
(2)培训前等级为“合格”与“优秀”的学生各有640×![]() =140名、
=140名、
640×![]() =20名
=20名
培训后等级为“合格”与“优秀”的学生各有640×![]() =320名、640×
=320名、640×![]() =160名
=160名
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.

(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过
 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=
 ,AH=3
,AH=3 ,求EM的值.
,求EM的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
 是某个体育馆(四面是墙)的平面图,长
是某个体育馆(四面是墙)的平面图,长 米,宽
米,宽 米.小明父子两人都沿着体育馆外围跑步,其中小明从
米.小明父子两人都沿着体育馆外围跑步,其中小明从 点沿
点沿 方向跑,同时父亲从
方向跑,同时父亲从 点出发,已知小明父亲的速度为6米/秒,小明的速度为4米/秒,若跑步过程中两人都没有回头跑,则经过______秒后,父亲第一次看到小明.
点出发,已知小明父亲的速度为6米/秒,小明的速度为4米/秒,若跑步过程中两人都没有回头跑,则经过______秒后,父亲第一次看到小明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个一元一次方程的一次项系数与常数项的差刚好是这个方程的解,则称这个方程为妙解方程.例如:方程
 中,
中, ,方程的解为
,方程的解为 ,则方程
,则方程 为妙解方程.请根据上述定义解答下列问题:
为妙解方程.请根据上述定义解答下列问题:(1)方程
 是妙解方程吗?试说明理由.
是妙解方程吗?试说明理由.(2)已知关于
 的一元一次方程
的一元一次方程 是妙解方程.求
是妙解方程.求 的值.
的值.(3)已知关于
 的一元一次方程
的一元一次方程 是妙解方程,并且它的解是
是妙解方程,并且它的解是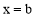 .求代数式
.求代数式 的值.
的值. -
科目: 来源: 题型:
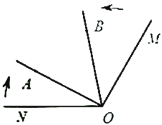
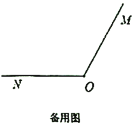
查看答案和解析>>【题目】如图,已知
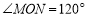 ,射线
,射线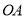 从
从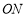 的位置开始绕点
的位置开始绕点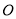 按顺时针方向旋转,速度是每秒
按顺时针方向旋转,速度是每秒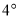 ,同时射线
,同时射线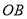 从
从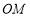 的位置开始绕点
的位置开始绕点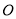 按逆时针方向旋转,速度是每秒
按逆时针方向旋转,速度是每秒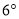 ,设旋转时间为
,设旋转时间为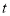 秒
秒 .
.
(1)用含
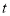 的代数式表示
的代数式表示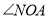 和
和 的度数;
的度数;(2)在旋转过程中,当
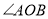 等于
等于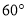 时,求
时,求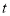 的值;
的值;(3)在旋转过程中是否存在这样的
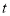 ,使得射线
,使得射线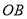 恰好是图中某个角的平分线?如果存在,请求出
恰好是图中某个角的平分线?如果存在,请求出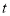 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. -
科目: 来源: 题型:
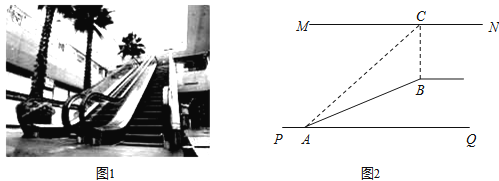
查看答案和解析>>【题目】如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
相关试题

