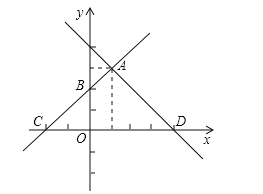
【题目】在如图所示的平面直角坐标系中,直线AB:y=k1x+b1与直线AD:y=k2x+b2相交于点A(1,3),且点B坐标为(0,2),直线AB交x轴负半轴于点C,直线AD交x轴正半轴于点D.
(1)求直线AB的函数解析式;
(2)若△ACD的面积为9,解不等式:k2x+b2>0;
(3)若点M为x轴一动点,当点M在什么位置时,使AM+BM的值最小?求出此时点M的坐标.
参考答案:
【答案】(1)y=x+2;(2)x<4;(3)(![]() ,0).
,0).
【解析】
(1)将点A、B两点代入,即可求解析式;
(2)令y=0,求出C点坐标,由三角形ACD的面积是9,求出D点坐标,结合图象即可求解;
(3)作点B关于x轴的对称点E(0,-2),连接AE交x轴于点M,设直线AE解析式为y=kx+b,确定AE的解析式即可求M点坐标.
解:(1)把A、B两点代入,得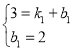 ,
,
解得![]() ,
,
故直线AB的函数解析式为y=x+2;
(2)令y=x+2=0得x=-2,
∴C(-2,0).
又∵△ACD的面积为9,
∴![]() 3×CD=9,
3×CD=9,
∴CD=6,
∴D点坐标(4,0),
由图象得不等式的解集为:x<4;
(3)作点B关于x轴的对称点E(0,-2),连接AE交x轴于点M,
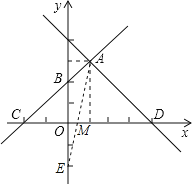
设直线AE解析式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴y=5x-2,
当y=0时,x=![]() ,故点M的坐标为(
,故点M的坐标为(![]() ,0).
,0).
-
科目: 来源: 题型:
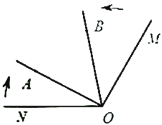
查看答案和解析>>【题目】如图,已知
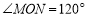 ,射线
,射线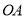 从
从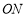 的位置开始绕点
的位置开始绕点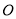 按顺时针方向旋转,速度是每秒
按顺时针方向旋转,速度是每秒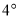 ,同时射线
,同时射线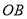 从
从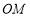 的位置开始绕点
的位置开始绕点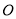 按逆时针方向旋转,速度是每秒
按逆时针方向旋转,速度是每秒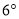 ,设旋转时间为
,设旋转时间为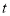 秒
秒 .
.
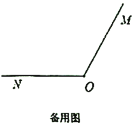
(1)用含
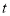 的代数式表示
的代数式表示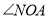 和
和 的度数;
的度数;(2)在旋转过程中,当
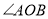 等于
等于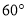 时,求
时,求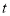 的值;
的值;(3)在旋转过程中是否存在这样的
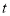 ,使得射线
,使得射线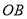 恰好是图中某个角的平分线?如果存在,请求出
恰好是图中某个角的平分线?如果存在,请求出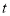 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
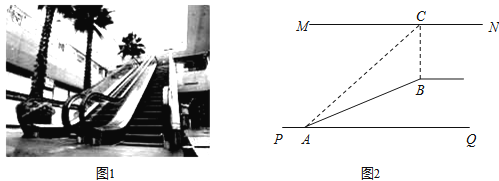
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.
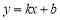 一定是一次函数
一定是一次函数B. 有的实数在数轴上找不到对应的点
C. 长为
 的三条线段能组成直角三角形
的三条线段能组成直角三角形D. 无论
 为何值,点
为何值,点 总是在第二象限
总是在第二象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地相距20
两地相距20 ,甲乙两人沿同一条路线从
,甲乙两人沿同一条路线从 地到
地到 地,如图的图象反映的是二人行进路程
地,如图的图象反映的是二人行进路程 (
( )与行进时间
)与行进时间 (
( )之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
)之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的图像反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x表示时间,y表示小明离他家的距离,若小明家、超市、书店在同一条直线上.
根据图像回答下列问题:

(1)超市离小明家多远,小明走到超市用了多少时间?
(2)超市离书店多远,小明在书店购书用了多少时间?
(3)书店离小明家多远,小明从书店走回家的平均速度是每分钟多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数
 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为 ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为 、
、 、
、 、
、 、
、 ,则
,则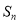 的值为______
的值为______ 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数

相关试题

