【题目】下列说法正确的是( )
A. ![]() 一定是一次函数
一定是一次函数
B. 有的实数在数轴上找不到对应的点
C. 长为![]() 的三条线段能组成直角三角形
的三条线段能组成直角三角形
D. 无论![]() 为何值,点
为何值,点![]() 总是在第二象限
总是在第二象限
参考答案:
【答案】D
【解析】
A根据一次函数定义进行分析,B根据实数与数轴上的点的对应关系进行分析,C根据勾股定理进行分析,D根据平面直角坐标系第二象限点的坐标特点进行分析.
A中![]() 是一次函数应满足k≠0,故错误;
是一次函数应满足k≠0,故错误;
B中实数与数轴上的点是一一对应的关系,所有的实数都能够在数轴上找到与之对应的点,故错误;
C中这三条线段不满足勾股定理,不能组成直角三角形,故错误;
D中在P点坐标中,横坐标为-2<0,纵坐标为![]() ,满足第二象限内点的坐标特点,所以无论x为何值,点P总是在第二象限,故正确.
,满足第二象限内点的坐标特点,所以无论x为何值,点P总是在第二象限,故正确.
故答案为:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个一元一次方程的一次项系数与常数项的差刚好是这个方程的解,则称这个方程为妙解方程.例如:方程
 中,
中, ,方程的解为
,方程的解为 ,则方程
,则方程 为妙解方程.请根据上述定义解答下列问题:
为妙解方程.请根据上述定义解答下列问题:(1)方程
 是妙解方程吗?试说明理由.
是妙解方程吗?试说明理由.(2)已知关于
 的一元一次方程
的一元一次方程 是妙解方程.求
是妙解方程.求 的值.
的值.(3)已知关于
 的一元一次方程
的一元一次方程 是妙解方程,并且它的解是
是妙解方程,并且它的解是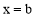 .求代数式
.求代数式 的值.
的值. -
科目: 来源: 题型:
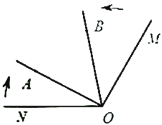
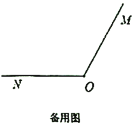
查看答案和解析>>【题目】如图,已知
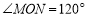 ,射线
,射线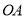 从
从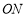 的位置开始绕点
的位置开始绕点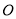 按顺时针方向旋转,速度是每秒
按顺时针方向旋转,速度是每秒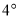 ,同时射线
,同时射线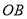 从
从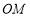 的位置开始绕点
的位置开始绕点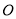 按逆时针方向旋转,速度是每秒
按逆时针方向旋转,速度是每秒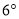 ,设旋转时间为
,设旋转时间为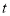 秒
秒 .
.
(1)用含
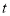 的代数式表示
的代数式表示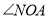 和
和 的度数;
的度数;(2)在旋转过程中,当
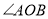 等于
等于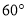 时,求
时,求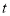 的值;
的值;(3)在旋转过程中是否存在这样的
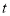 ,使得射线
,使得射线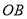 恰好是图中某个角的平分线?如果存在,请求出
恰好是图中某个角的平分线?如果存在,请求出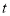 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
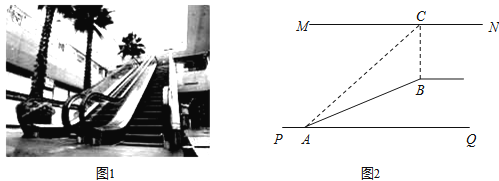
-
科目: 来源: 题型:
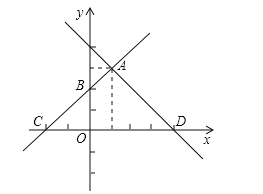
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,直线AB:y=k1x+b1与直线AD:y=k2x+b2相交于点A(1,3),且点B坐标为(0,2),直线AB交x轴负半轴于点C,直线AD交x轴正半轴于点D.
(1)求直线AB的函数解析式;
(2)若△ACD的面积为9,解不等式:k2x+b2>0;
(3)若点M为x轴一动点,当点M在什么位置时,使AM+BM的值最小?求出此时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地相距20
两地相距20 ,甲乙两人沿同一条路线从
,甲乙两人沿同一条路线从 地到
地到 地,如图的图象反映的是二人行进路程
地,如图的图象反映的是二人行进路程 (
( )与行进时间
)与行进时间 (
( )之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
)之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②甲用了5个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的图像反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x表示时间,y表示小明离他家的距离,若小明家、超市、书店在同一条直线上.
根据图像回答下列问题:

(1)超市离小明家多远,小明走到超市用了多少时间?
(2)超市离书店多远,小明在书店购书用了多少时间?
(3)书店离小明家多远,小明从书店走回家的平均速度是每分钟多少米?
相关试题

