【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图. 
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
参考答案:
【答案】
(1)解:根据题意得:
得4分的学生有50×50%=25(人),
答:得4分的学生有25人
(2)解:根据题意得:
平均分= ![]() =3.7(分)
=3.7(分)
(3)解:设第二次测试中得4分的学生有x人,得5分的学生有y人,根据题意得:
![]() ,
,
解得: ![]() ,
,
答:第二次测试中得4分的学生有15人,得5分的学生有30人
【解析】(1)用总人数乘以得4分的学生所占的百分百即可得出答案;(2)根据平均数的计算公式把所有人的得分加起来,再除以总人数即可;(3)先设第二次测试中得4分的学生有x人,得5分的学生有y人,再根据成绩的最低分为3分,得4分和5分的人数共有45人,平均分比第一次提高了0.8分,列出方程组,求出x,y的值即可.
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中建立如图的平面直角坐标系 xOy,△ABC 的三个顶点 都在格点上,点 A的坐标是(4,4),请解答下列问题:
(1)将△ABC 向下平移 5 单位长度,画出平移后的△A1B1C1并写出点 A对应点A1的坐标;
(2)画出△A1B1C1 关于 y 轴对称的△A2B2C2 并写出 A2 的坐标;
(3)求S△ABC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育商店购进一批甲、乙两种足球,已知3个甲种足球的进价与2个乙种足球的进价的和为142元,2个甲种足球的进价与4个乙种足球的进价的和为164元.
(1)求每个甲、乙两种足球的进价分别是多少?
(2)如果购进甲种足球超过10个,超出部分可以享受7折优惠.商场决定在甲、乙两种足球选购其中一种,且数量超过10个,试帮助体育商场判断购进哪种足球省钱. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x= . ①求该抛物线的函数解析式;
. ①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.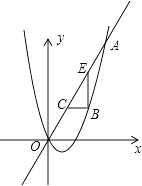
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
(4)将射线OA绕原点旋转45°并与抛物线交于点P,求出P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A是x轴正半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连结AC,BC,CD,设点A的横坐标为t.

(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段BD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到△C′D′F′,再将A,B,C′,D′为顶点的四边形沿C′F′剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的点C′的坐标.
相关试题

