【题目】如图1,点A是x轴正半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连结AC,BC,CD,设点A的横坐标为t.
(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段BD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到△C′D′F′,再将A,B,C′,D′为顶点的四边形沿C′F′剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的点C′的坐标.
参考答案:
【答案】
(1)
解:由题意,易证Rt△ACF∽Rt△BAO,
∴ ![]() .
.
∵AB=2AM=2AC,
∴CF= ![]() OA=
OA= ![]() t.
t.
当t=2时,CF=1
(2)
解:①由(1)知,Rt△ACF∽Rt△BAO,
∴ ![]() ,
,
∴AF= ![]() OB=2,
OB=2,
∴FD=AF=2,.
∵点C落在线段BD上,
∴△DCF∽△DBO,
∴ ![]() ,即
,即 ![]() ,
,
解得t= ![]() ﹣2或t=﹣
﹣2或t=﹣ ![]() ﹣2(小于0,舍去)
﹣2(小于0,舍去)
∴当t= ![]() ﹣2时,点C落在线段BD上;
﹣2时,点C落在线段BD上;
②当0<t<8时,如题图1所示:
S= ![]() BECE=
BECE= ![]() (t+2)(4﹣
(t+2)(4﹣ ![]() t)=-
t)=- ![]() t2+
t2+ ![]() t+4;
t+4;
当t>8时,如答图1所示:
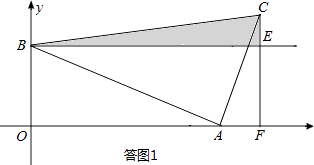
S= ![]() BECE=
BECE= ![]() (t+2)(
(t+2)( ![]() t﹣4)=
t﹣4)= ![]() t2﹣
t2﹣ ![]() t﹣4
t﹣4
(3)
解:符合条件的点C的坐标为:(12,4),(8,4)或(2,4).
理由如下:
在△CDF沿x轴左右平移的过程中,符合条件的剪拼方法有三种:
方法一:如答图2所示,当F′C′=AF′时,点F′的坐标为(12,0),
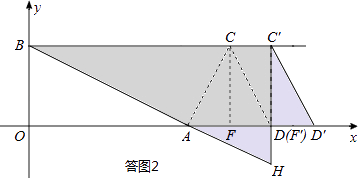
根据△C′D′F′≌△AHF′,△BC′H为拼成的三角形,此时C′的坐标为(12,4);
方法二:如答图3所示,当点F′与点A重合时,点F′的坐标为(8,0),

根据△OC′A≌△BAC′,可知△OC′D′为拼成的三角形,此时C′的坐标为(8,4);
方法三:当BC′=F′D′时,点F′的坐标为(2,0),
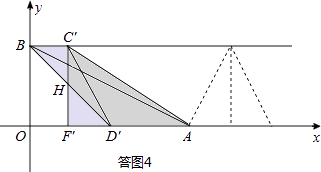
根据△BC′H≌△D′F′H,可知△AF′C′为拼成的三角形,此时C′的坐标为(2,4)
【解析】(1)由Rt△ACF∽Rt△BAO,得CF= ![]() OA=
OA= ![]() t,由此求出CF的值;(2)①由Rt△ACF∽Rt△BAO,可以求得AF的长度;若点C落在线段BD上,则有△DCF∽△DBO,根据相似比例式列方程求出t的值;
t,由此求出CF的值;(2)①由Rt△ACF∽Rt△BAO,可以求得AF的长度;若点C落在线段BD上,则有△DCF∽△DBO,根据相似比例式列方程求出t的值;
②有两种情况,需要分类讨论:当0<t≤8时,如题图1所示;当t>8时,如答图1所示.(3)本问涉及图形的剪拼.在△CDF沿x轴左右平移的过程中,符合条件的剪拼方法有三种,需要分类讨论,分别如答图2﹣4所示.
【考点精析】本题主要考查了相似图形和相似三角形的判定与性质的相关知识点,需要掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.

根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x= . ①求该抛物线的函数解析式;
. ①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.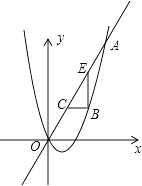
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
(4)将射线OA绕原点旋转45°并与抛物线交于点P,求出P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.

(1)判断△ABC的形状:;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-102n×100×(-10)2n-1;
(2)[(-a)·(-b)2·a2b3c]2;
(3)(x3)2÷x2÷x-x3÷(-x)4·(-x4);
(4)(-9)3×
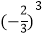 ×
× ;
;(5)xn+1·xn-1·x÷xm;
(6)a2·a3-(-a2)3-2a·(a2)3-2[(a3)3÷a3].
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y=﹣2x﹣2
(1)根据关系式画出函数的图象.
(2)求出图象与 x 轴、y 轴的交点 A、B 的坐标.
(3)求 A、B 两点间的距离.
(4)y 的值随 x 值的增大怎样变化?

相关试题

