【题目】如图所示,动点A,B同时从原点O出发,运动的速度都是每秒1个单位,动点A沿x轴正方向运动,动点B沿y轴正方向运动,以OA,OB为邻边建立正方形OACB,抛物线y=﹣x2+bx+c经过B,C两点,假设A,B两点运动的时间为t秒: 根据
根据
(1)直接写出直线OC的解析式;
(2)当t=3秒时,求此时抛物线的解析式;此时抛物线上是否存在一点D,使得S△BCD=6?若存在,求出点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,有一条平行于y轴的动直线l,交抛物线于点E,交直线OC于点F,若以O、B、E、F四个点构成的四边形是平行四边形,求点F的坐标;
(4)在动点A、B运动的过程中,若正方形OACB内部有一个点P,且满足OP= ![]() ,CP=2,∠OPA=135°,直接写出此时AP的长度.
,CP=2,∠OPA=135°,直接写出此时AP的长度.
参考答案:
【答案】
(1)解:∵四边形OABC是正方形,
∴∠AOC=45°,
∴直线OC的解析式为y=x
(2)解:∵t=3秒,
∴OA=OB=3,
∴点B(0,3),C(3,3),
将点B、C代入抛物线得, ![]() ,
,
解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+3x+3,
设BC边上的高为h,
∵BC=OA=3,S△BCD=6,
∴h=4,
∴点D的纵坐标为3﹣4=﹣1,
令y=﹣1,则﹣x2+3x+3=﹣1,
整理得,x2﹣3x﹣4=0,
解得x1=﹣1,x2=4,
所以,D1(﹣1,﹣1),D2(4,﹣1)
(3)解:∵OB=3,
∴EF=3,
设E(m,﹣m2+3m+3),F(m,m),
若E在F上方,则,﹣m2+3m+3﹣m=3,
整理得,m2﹣2m=0,
解得m1=0(舍去),m2=2,
∴F1(2,2),
若F在E上方,则,m﹣(﹣m2+3m+3)=3,
整理m2﹣2m﹣6=0,
解得m1=1﹣ ![]() ,m2=1+
,m2=1+ ![]() ,
,
∴F2(1﹣ ![]() ,1﹣
,1﹣ ![]() ),
),
F3(1+ ![]() ,1+
,1+ ![]() )
)
(4)解:如图,将△AOP绕点A逆时针旋转90°得到△AP′C,
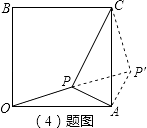
由旋转的性质得,AP′=AP,P′C=OP= ![]() ,∠AP′C=∠OPA=135°,
,∠AP′C=∠OPA=135°,
∵△APP′是等腰直角三角形,
∴∠AP′P=45°,
∴∠PP′C=135°﹣45°=90°,
由勾股定理得,PP′= ![]() =
= ![]() =
= ![]() ,
,
所以,AP= ![]() PP′=
PP′= ![]() ×
× ![]() =1.
=1.
【解析】(1)由正方形的性质得出∠AOC=45°。易得直线OC的解析式为y=x.
(2)根据已知求出点B、C两点的坐标,用待定系数法就可以求出二次函数的解析式。设BC边上的高为h,根据三角形的面积求出h的值,即可求出点D的纵坐标,将点D的纵坐标代入函数解析式就可以 求出点D的坐标。
(3)已知O、B、E、F四个点构成的四边形是平行四边形,则有OB=EF=3,点E在抛物线上,点F在直线y=x上,分两种情况:点E在点F的上方;点E在点F的下方,设出点E、F的坐标,根据OB=EF,建立方程求解,即可求出点F的坐标。
(4)此题用旋转的知识来解答。将△AOP绕点A逆时针旋转90°得到△AP′C,易证明APP′是等腰直角三角形,再求出∠PP′C=90°,利用勾股定理就可以求出AP的长。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x一1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值.
(1)(x-1)(x+1) =_____________;
(2)(x—1)( x2+x+1) =_____________;
(3)(x-1)(x3+ x2+x+1) =____________;
…
由此我们可以得到:
(4)(x一1)( x99+x98+x97+…+x+1) =___________,
请你利用上面的结论,完成下列的计算:
(5)299+298+297+…+2+1;
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别从
 ,
, 两地相向而行,他们距
两地相向而行,他们距 地的距离
地的距离 与时间
与时间 的关系如图所示,下列说法错误的是( )
的关系如图所示,下列说法错误的是( )
A.甲的速度是
 B.甲出发4.5小时后与乙相遇
B.甲出发4.5小时后与乙相遇C.乙比甲晚出发2小时D.乙的速度是

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的角平分线,
的角平分线, 于点
于点 ,
, 于点
于点 ,连接
,连接 交
交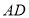 于
于 .有以下三个结论:①
.有以下三个结论:① ;②
;② ;③当
;③当 时,四边形
时,四边形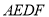 是正方形;④
是正方形;④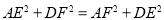 .其中正确的是( )
.其中正确的是( )
A.②③B.②④C.①③④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )

A.90°
B.110°
C.120°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
1、计算、 +(
+( )﹣1﹣4tan45° 2、 解方程:x2=3x.
)﹣1﹣4tan45° 2、 解方程:x2=3x.
(1)计算: +(
+(  )﹣1﹣4tan45°
)﹣1﹣4tan45°
(2)解方程:x2=3x.
相关试题

