搜索
【题目】如图，四边形ABCD，∠A=110°，若点D在AB、AC的垂直平分线上，则∠BDC为（ ）
A.90°
B.110°
C.120°
D.140°
参考答案：
【答案】D
【解析】解：
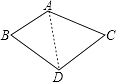
连接AD，
∵点D在AB、AC的垂直平分线上，
∴BD=AD，DC=AD，
∴∠B=∠BAD，∠C=∠CAD，
∵∠BAC=110°=∠BAD+∠CAD，
∴∠B+∠C=110°，
∴∠BDC=360°﹣（∠B+∠C）﹣∠BAC=360°﹣110°﹣110°=140°，
所以答案是：D．
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人分别从
，
两地相向而行，他们距地的距离
与时间
的关系如图所示，下列说法错误的是（ ）
A.甲的速度是
B.甲出发4.5小时后与乙相遇C.乙比甲晚出发2小时D.乙的速度是
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
是
的角平分线，
于点
，
于点
，连接
交于
．有以下三个结论：①
；②
；③当
时，四边形
是正方形；④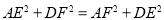
．其中正确的是（ ）
A.②③B.②④C.①③④D.②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，动点A，B同时从原点O出发，运动的速度都是每秒1个单位，动点A沿x轴正方向运动，动点B沿y轴正方向运动，以OA，OB为邻边建立正方形OACB，抛物线y=﹣x2+bx+c经过B，C两点，假设A，B两点运动的时间为t秒：
根据
（1）直接写出直线OC的解析式；
（2）当t=3秒时，求此时抛物线的解析式；此时抛物线上是否存在一点D，使得S△BCD=6？若存在，求出点D的坐标；若不存在，说明理由；
（3）在（2）的条件下，有一条平行于y轴的动直线l，交抛物线于点E，交直线OC于点F，若以O、B、E、F四个点构成的四边形是平行四边形，求点F的坐标；
（4）在动点A、B运动的过程中，若正方形OACB内部有一个点P，且满足OP=
，CP=2，∠OPA=135°，直接写出此时AP的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将矩形纸片的两只直角分别沿EF、DF翻折，点B恰好落在AD边上的点B′处，点C恰好落在边B′F上．若AE=3，BE=5，则FC= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
1、计算、
+（
）﹣1﹣4tan45° 2、 解方程：x2=3x．
（1）计算： +（ ）﹣1﹣4tan45°
（2）解方程：x2=3x． -
科目： 来源： 题型：
查看答案和解析>>【题目】若（x2+3mx﹣
）（x2﹣3x+n）的积中不含x和x3项，（1）求m2﹣mn+
n2的值；（2）求代数式（﹣18m2n）2+（9mn）﹣2+（3m）2014n2016的值．
相关试题
