【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点P从点B出发,沿BC向点C匀速运动,速度为1cm/s;过点P作PD∥AB,交AC于点D,同时,点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动,连接PQ.设运动时间为t(s)(0<t<2.5),解答下列问题:
(1)当t为何值时,四边形ADPQ为平行四边形?
(2)设四边形ADPQ的面积为y(cm2),试确定y与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S四边形ADPQ:S△PQB=13:2?若存在,请说明理由,若存在,求出t的值,并求出此时PQ的距离.
参考答案:
【答案】
(1)
解:∵∠C=90°,AC=3cm,BC=4cm,
∴AB= ![]() =5cm,
=5cm,
∵PD∥AB,
∴当PQ∥AC时,四边形ADPQ是平行四边形,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,t= ![]() ,
,
答:当t= ![]() 时,四边形ADPQ为平行四边形
时,四边形ADPQ为平行四边形
(2)
解:过点P作PE⊥AB,垂足为E,

∵∠PEB=∠C=90°,
∠B=∠B,
∴△BPE∽△BCA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,PE= ![]() t,
t,
∵PD∥AB,
∴∠DPC=∠B,
∠C=∠C,
∴△CPD∽△CBA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,PD= ![]() ,
,
∴y=S四边形ADPQ= ![]() ×(PD+AQ)×PE
×(PD+AQ)×PE
= ![]() ×(
×( ![]() +2t)×
+2t)× ![]() t
t
= ![]() t2+
t2+ ![]() t
t
(3)
解:若存在某一时刻,使S四边形ADPQ:S△PQB=13:2,
则y= ![]() S△PQB
S△PQB
∵S△PQB= ![]() QB×PE=﹣
QB×PE=﹣ ![]() t2+
t2+ ![]() t,
t,
∴ ![]() t2+
t2+ ![]() t=
t= ![]() (﹣
(﹣ ![]() t2+
t2+ ![]() t),
t),
解得,t1=0(舍去),t2=2,
则t为2s时,S四边形ADPQA:S△PQB=13:2,
当t=2时,BP=2,BQ=5﹣4=1,
作QH⊥BC于H,
则QH= ![]() ,BH=
,BH= ![]() ,
,
∴PH= ![]() ,
,
则PQ= ![]() =
= ![]() .
.

【解析】(1)根据勾股定理求出AB,根据平行四边形的性质得到PQ∥AC,根据相似三角形的性质列出比例式,计算即可;(2)过点P作PE⊥AB,证明△BPE∽△BCA,根据相似三角形的性质求出PE、PD,根据梯形的面积公式计算即可;(3)根据题意列出一元二次方程,解方程求出t,根据相似三角形的性质、勾股定理计算即可.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出:用水平线和竖直线将平面分成若干个面积为1的小长方形格子,小长方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x,多边形内部的格点数为n,S与x,n之间是否存在一定的数量关系呢?
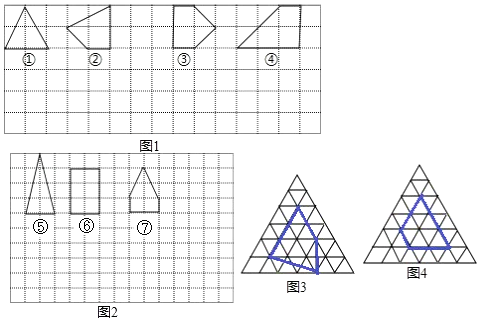
(1)问题探究:
如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S= .多边形的序号
①
②
③
④
…
多边形的面积S
2
2.5
3
4
…
各边上格点的个数和x
4
…
(2)在图2中所示的格点多边形,这些多边形内部都有且只有2个格点.探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S= .
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=(用含有字母x,n的代数式表示)
(4)问题拓展:
请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:格点多边形各边上的格点的个数
格点多边形内部的格点个数
格点多边形的面积
多边形1(图3)
8
1
8
多边形2(图4)
7
3
11
…
…
…
…
…
…
…
…
…
…
…
…
一般格点多边形
a
b
S
则S与a,b之间的关系为S=(用含a,b的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式
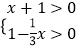 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.
B.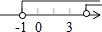
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( ) ①AB∥CQ;②∠ACQ=60°;③AP2=AMAC;④若BP=PC,则PQ⊥AC.
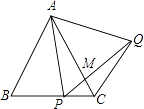
A.①②
B.①③
C.①②③
D.①②③④ -
科目: 来源: 题型:
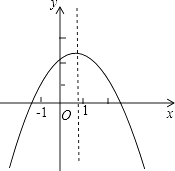
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个
相关试题

