【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

参考答案:
【答案】(1)证明见解析(2)BD=6cm.
【解析】
(1)证两条线段相等,通常用全等,本题中的AE和CD分别在三角形AEC和三角形CDB中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答;
(2)由(1)得BD=EC=![]() BC=
BC=![]() AC,且AC=12cm,即可求出BD的长.
AC,且AC=12cm,即可求出BD的长.
(1)∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°,
∴∠D=∠AEC,
又∵∠DBC=∠ECA=90°,
且BC=CA,
∴△DBC≌△ECA(AAS),
∴AE=CD;
(2)因为△ACE ≌△CBD,所以BD =CE,
因为CE=![]() BC=
BC=![]() AC=
AC=![]() ×12=6cm,
×12=6cm,
所以BD =6cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
A. 钱
钱
B. 钱
钱
C.1钱
D. 钱
钱 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B为抛物线E:y2=2px(p>0)上异于顶点O的两点,△AOB是等边三角形,其面积为48
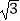 ,则p的值为( )
,则p的值为( )
A.2
B.2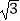
C.4
D.4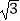
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 sin(2x+φ)+cos(2x+φ)为偶函数,且在[0,
sin(2x+φ)+cos(2x+φ)为偶函数,且在[0,  ]上是增函数,则φ的一个可能值为( )
]上是增函数,则φ的一个可能值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰梯形ABCD中,AB∥DC、CD=2AB=4,∠A=
 ,向量
,向量  、
、 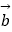 满足
满足 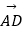 =2
=2  ,
,  =2
=2  +
+ 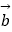 ,则下列式子不正确的是( )
,则下列式子不正确的是( )
A.|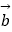 |=2
|=2
B.|2 |=2
|=2 
C.2 =﹣2
=﹣2
D. =1
=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an} 满足a1=
 ,a2=
,a2=  ,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*),数列{an}的前n项和为Sn , 则S2017= .
,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*),数列{an}的前n项和为Sn , 则S2017= . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A、B、C的对边分别为a,b,c,且bcosC=(2a﹣c)cosB.
(1)求角B的大小;
(2)已知b= ,BD为AC边上的高,求BD的取值范围.
,BD为AC边上的高,求BD的取值范围.
相关试题

