【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ) 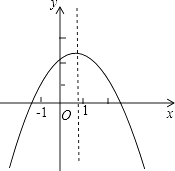
A.4个
B.3个
C.2个
D.1个
参考答案:
【答案】C
【解析】解:①∵抛物线开口向下, ∴a<0,
∵﹣ ![]() <1,
<1,
∴2a+b<0,①正确;
②抛物线与y轴交于正半轴,
∴c>0,
∵﹣ ![]() >0,a<0,
>0,a<0,
∴b>0,
∴abc<0,②错误;
③当x=﹣2时,y<0,
∴4a﹣2b+c<0,③错误;
x=±1时,y>0,
∴a﹣b+c>0,a+b+c>0,
∴a+c>0,④正确,
故选:C.
【考点精析】认真审题,首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点P从点B出发,沿BC向点C匀速运动,速度为1cm/s;过点P作PD∥AB,交AC于点D,同时,点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动,连接PQ.设运动时间为t(s)(0<t<2.5),解答下列问题:

(1)当t为何值时,四边形ADPQ为平行四边形?
(2)设四边形ADPQ的面积为y(cm2),试确定y与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S四边形ADPQ:S△PQB=13:2?若存在,请说明理由,若存在,求出t的值,并求出此时PQ的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式
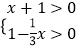 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.
B.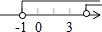
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( ) ①AB∥CQ;②∠ACQ=60°;③AP2=AMAC;④若BP=PC,则PQ⊥AC.
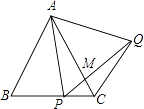
A.①②
B.①③
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
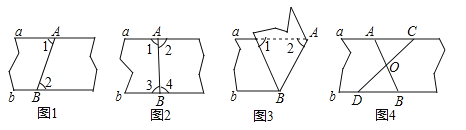
A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
相关试题

