【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

参考答案:
【答案】(1)8;(2)①DF=17;②a的值为10或12或![]() .
.
【解析】
(1)作AM⊥BC于M,根据三角形的面积公式计算;
(2)①根据勾股定理求出BM、AC,根据平移的性质解答;
②分AB=BE、AB=AE、EA=EB三种情况,根据勾股定理计算即可.
(1)作AM⊥BC于M,
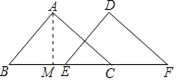
∵△ABC的面积为84,
∴![]() ×BC×AM=84,
×BC×AM=84,
解得,AM=8,即BC边上的高为8;
(2)①在Rt△ABM中,BM=![]() ,
,
∴CM=BC﹣BM=15,
在Rt△ACM中,AC=![]() =17,
=17,
由平移的性质可知,DF=AC=17;
②当AB=BE=10时,a=BE=10;
当AB=AE=10时,BE=2BM=12,
则a=BE=12;
当EA=EB=a时,ME=a﹣6,
在Rt△AME中,AM2+ME2=AE2,
即82+(a﹣6)2=a2,
解得,a=![]() ,
,
则当△ABE时等腰三角形时,a的值为10或12或![]() .
.
-
科目: 来源: 题型:
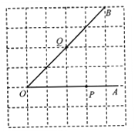
查看答案和解析>>【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具,
(1)设该种品牌玩具的销售单价为x元,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元;
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于45元,且商场要完成不少于480件的销售任务,求商场销售该品牌玩具获得的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出:用水平线和竖直线将平面分成若干个面积为1的小长方形格子,小长方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x,多边形内部的格点数为n,S与x,n之间是否存在一定的数量关系呢?
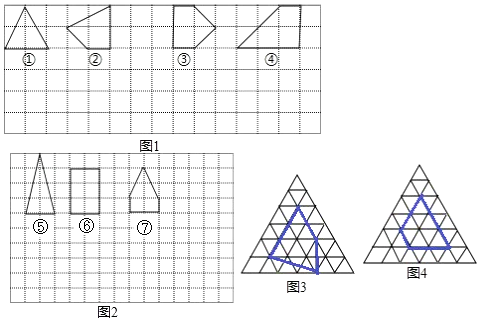
(1)问题探究:
如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S= .多边形的序号
①
②
③
④
…
多边形的面积S
2
2.5
3
4
…
各边上格点的个数和x
4
…
(2)在图2中所示的格点多边形,这些多边形内部都有且只有2个格点.探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S= .
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=(用含有字母x,n的代数式表示)
(4)问题拓展:
请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:格点多边形各边上的格点的个数
格点多边形内部的格点个数
格点多边形的面积
多边形1(图3)
8
1
8
多边形2(图4)
7
3
11
…
…
…
…
…
…
…
…
…
…
…
…
一般格点多边形
a
b
S
则S与a,b之间的关系为S=(用含a,b的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点P从点B出发,沿BC向点C匀速运动,速度为1cm/s;过点P作PD∥AB,交AC于点D,同时,点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动,连接PQ.设运动时间为t(s)(0<t<2.5),解答下列问题:

(1)当t为何值时,四边形ADPQ为平行四边形?
(2)设四边形ADPQ的面积为y(cm2),试确定y与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S四边形ADPQ:S△PQB=13:2?若存在,请说明理由,若存在,求出t的值,并求出此时PQ的距离.
相关试题

