Question

【题目】在平面直角坐标系，直线y=2x+2交x轴于A，交y轴于 D，

（1）直接写直线y=2x+2与坐标轴所围成的图形的面积

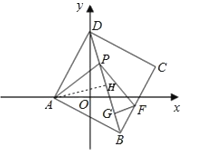
（2）以AD为边作正方形ABCD，连接AD，P是线段BD上（不与B，D重合）的一点，在BD上截取PG=，过G作GF垂直BD，交BC于F，连接AP．

问：AP与PF有怎样的数量关系和位置关系？并说明理由；

（3）在（2）中的正方形中，若∠PAG=45°，试判断线段PD，PG，BG之间有何关系，并说明理由．

Answer 1

【答案】（1）1；（2）AP=PF且AP⊥PF，理由见解析；（3）PD2+BG2=PG2，理由见解析

【解析】

（1）先根据一次函数解析式求出A,D的坐标，根据三角形的面积公式即可求解；

（2）过点A作AH⊥DB，先计算出AD=，根据正方形的性质得到BD=，AH=DH=BD=，由PG=，得到DP+BG=，则PH=BG,可证得Rt△APH≌Rt△PFG，即可得到AP=PF且AP⊥PF；

（3）把△AGB绕点A点逆时针旋转90°得到△AMD，可得∠MDA=∠ABG=45°，DM=BG, ∠MAD=∠BAG,AM=AG,则∠MDP=90°，根据勾股定理有DP2+BG2=PM2,由∠PAG=45°，可得∠DAP+∠BAG=45°，即∠MAP=45°，易证得△AMP≌△AGP，得到MP=PG,即可DP2+BG2=PM2．

（1）∵直线y=2x+2交x轴于A，交y轴于 D，

令x=0，解得y=2，∴D（0，2）

令y=0，解得x=-1，∴A（-1，0）

∴AO=1，DO=2，

∴直线y=2x+2与坐标轴所围成的图形△AOD=×1×2=1；

（2）AP=PF且AP⊥PF，理由如下：

过点A作AH⊥DB，如图，

∵A（-1，0），D（0，2）

∴AD===AB，

∵四边形ABCD是正方形

∴BD==，

∴AH=DH=BD=，

而PG=，

∴DP+BG=，

而DH=DP+PH=

∴PH=BG,

∵∠GBF=45°

∴BG=GF=HP

∴Rt△APH≌Rt△PFG，

∴AP=PF, ∠PAH=∠PFG

∴∠APH+∠GPF=90°即AP⊥PF；

（3）PD2+BG2=PG2，理由如下：

如图，把△AGB绕点A点逆时针旋转90°得到△AMD，连接MP，

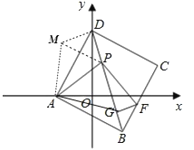
∴∠MDA=∠ABG=45°，DM=BG, ∠MAD=∠BAG,AM=AG,

∴∠MDP=90°，

∴DP2+BG2=PM2,

又∵∠PAG=45°，

∴∠DAP+∠BAG=45°，

∴∠MAD+∠DAP =45°，即∠MAP=45°，

而AM=AG，

∴△AMP≌△AGP，

∴MP=PG,

∴PD2+BG2=PG2