搜索
【题目】商场准备购进甲.乙两种商品，若购进甲商品80个，乙商品40个，需要800元；若购进甲商品50个，乙商品30个，需要550元.
（1）求商场购进甲.乙两种商品每个需要多少元？
（2）商场准备1000元全部用来购进甲.乙两种商品，计划销售每个甲种商品可获利润4元，销售每个乙种商品可获利润5元，销售这两种玩具的总利润不低于600元，那么商场最多购进乙种商品多少个?
参考答案：
【答案】（1）甲5元/个，乙10元/个；（2）66个
【解析】
（1）设甲种玩具每个x元，乙种玩具每个y元，根据：①甲种玩具80个费用+乙种玩具40个的费用=800元，②甲种玩具50个费用+乙种玩具30个费用=550元，列方程组求解即可；
（2）设购进乙种玩具a个，则购进甲种玩具
=200-2a（个），根据销售这两种玩具的总利润不低于600元建立不等式求出其解即可．
（1）设甲种玩具每个x元，乙种玩具每个y元，
根据题意，得：
，
解得：
，
答：甲种玩具每个5元，乙种玩具每个10元．
（2）设购进乙种玩具a个，则甲种玩具=200-2a（个），
根据题意，得：4（200-2a）+5a≥600，
解得：a≤66
，
∵a是正整数，
∴a的最大值为66，
答：这个玩具店需要最多购进乙种玩具66个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD是BC上的中线，点E在线段AC上且EC=2AE，线段AD与线段BE交于点F，若△ABC对面积为3，则四边形EFDC的面积为__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系，直线y=2x+2交x轴于A，交y轴于 D，
（1）直接写直线y=2x+2与坐标轴所围成的图形的面积
（2）以AD为边作正方形ABCD，连接AD，P是线段BD上（不与B，D重合）的一点，在BD上截取PG=
，过G作GF垂直BD，交BC于F，连接AP．问：AP与PF有怎样的数量关系和位置关系？并说明理由；
（3）在（2）中的正方形中，若∠PAG=45°，试判断线段PD，PG，BG之间有何关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
，
，
是边
上的两点，且有
，则图中等腰三角形的个数是（ ）
A.2B.6C.5D.7
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，在△ABC中，∠B＜∠C，AD，AE分别是△ABC的高和角平分线，
（1）若∠B=30°，∠C=50°．则∠DAE的度数是 ．（直接写出答案）
（2）写出∠DAE、∠B、∠C的数量关系： ，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
，
，
，作斜边AB上中线CD，得到第1个三角形ACD；
于点E，作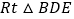
斜边DB上中线EF，得到第2个三角形DEF；依次作下去
则第1个三角形的面积等于______，第n个三角形的面积等于______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)，B(3,2).
(1)求m的值和抛物线的解析式；
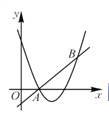
(2)求不等式x2+bx+c>x+m的解集(直接写出答案)；
(3)若M(a,y1),N(a+1,y2)两点都在抛物线y=x2+bx+c上，试比较y1与y2的大小.
相关试题
