【题目】如图,直线y=﹣ ![]() x+
x+ ![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+ ![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
参考答案:
【答案】
(1)
解:∵直线y=﹣ ![]() x+
x+ ![]() 分别与x轴、y轴交于B、C两点,
分别与x轴、y轴交于B、C两点,
∴B(3,0),C(0, ![]() ),
),
∴OB=3,OC= ![]() ,
,
∴tan∠BCO= ![]() =
= ![]() ,
,
∴∠BCO=60°,
∵∠ACB=90°,
∴∠ACO=30°,
∴ ![]() =tan30°=
=tan30°= ![]() ,即
,即 ![]() =
= ![]() ,解得AO=1,
,解得AO=1,
∴A(﹣1,0);
(2)
解:∵抛物线y=ax2+bx+ ![]() 经过A,B两点,
经过A,B两点,
∴ ![]() ,解得
,解得 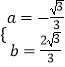 ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ;
;
(3)
解:∵MD∥y轴,MH⊥BC,
∴∠MDH=∠BCO=60°,则∠DMH=30°,
∴DH= ![]() DM,MH=
DM,MH= ![]() DM,
DM,
∴△DMH的周长=DM+DH+MH=DM+ ![]() DM+
DM+ ![]() DM=
DM= ![]() DM,
DM,
∴当DM有最大值时,其周长有最大值,
∵点M是直线BC上方抛物线上的一点,
∴可设M(t,﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() ),则D(t,﹣
),则D(t,﹣ ![]() t+
t+ ![]() ),
),
∴DM=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() ),则D(t,﹣
),则D(t,﹣ ![]() t+
t+ ![]() ),
),
∴DM=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() ﹣(﹣
﹣(﹣ ![]() t+
t+ ![]() )=﹣
)=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,DM有最大值,最大值为
时,DM有最大值,最大值为 ![]() ,
,
此时 ![]() DM=
DM= ![]() ×
× ![]() =
= ![]() ,
,
即△DMH周长的最大值为 ![]() .
.
【解析】(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH的周长,利用二次函数的性质可求得其最大值.
【考点精析】通过灵活运用二次函数的最值和平行线的性质,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
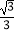 x﹣
x﹣ 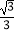 与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 .
与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 . 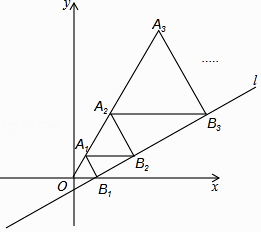
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的周长为16,面积为8
 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 . 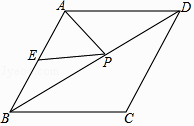
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.

(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=
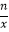 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3. 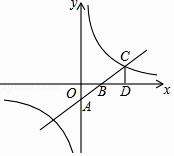
(1)求一次函数与反比例函数的解析式;
(2)直接写出当x>0时,kx+b﹣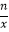 <0的解集.
<0的解集.
相关试题

