【题目】如图,在平面直角坐标系中,直线l:y= ![]() x﹣
x﹣ ![]() 与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 .
与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 . 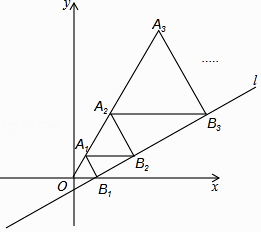
参考答案:
【答案】![]()
【解析】解:由直线l:y= ![]() x﹣
x﹣ ![]() 与x轴交于点B1 , 可得B1(1,0),D(﹣
与x轴交于点B1 , 可得B1(1,0),D(﹣ ![]() ,0),
,0),
∴OB1=1,∠OB1D=30°,
如图所示,过A1作A1A⊥OB1于A,则OA= ![]() OB1=
OB1= ![]() ,
,
即A1的横坐标为 ![]() =
= ![]() ,
,
由题可得∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,
∴∠A1B1B2=90°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B= ![]() A1B2=1,
A1B2=1,
即A2的横坐标为 ![]() +1=
+1= ![]() =
= ![]() ,
,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C= ![]() A2B3=2,
A2B3=2,
即A3的横坐标为 ![]() +1+2=
+1+2= ![]() =
= ![]() ,
,
同理可得,A4的横坐标为 ![]() +1+2+4=
+1+2+4= ![]() =
= ![]() ,
,
由此可得,An的横坐标为 ![]() ,
,
∴点A2017的横坐标是 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】通过灵活运用等边三角形的性质和含30度角的直角三角形,掌握等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )
A.
B.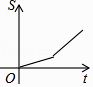
C.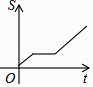
D.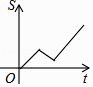
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(x﹣y)2=x2﹣y2
B.| ﹣2|=2﹣
﹣2|=2﹣ 
C. ﹣
﹣  =
= 
D.﹣(﹣a+1)=a+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的周长为16,面积为8
 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 . 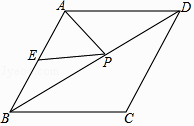
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+
x+  分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+  经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
相关试题

