【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 . 
参考答案:
【答案】①②③
【解析】解:①∵OC⊥AB, ∴∠BOC=∠AOC=90°.
∵OC=OA,
∴∠OCA=∠OAC=45°.
∵AC∥OD,
∴∠BOD=∠CAO=45°,
∴∠DOC=45°,
∴∠BOD=∠DOC,
∴OD平分∠COB.故①正确;
②∵∠BOD=∠DOC,
∴BD=CD.故②正确;
③∵∠AOC=90°,
∴∠CDA=45°,
∴∠DOC=∠CDA.
∵∠OCD=∠OCD,
∴△DOC∽△EDC,
∴ ![]() ,
,
∴CD2=CECO.故③正确.
所以答案是:①②③.
【考点精析】本题主要考查了圆周角定理和相似三角形的判定与性质的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(x﹣y)2=x2﹣y2
B.| ﹣2|=2﹣
﹣2|=2﹣ 
C. ﹣
﹣  =
= 
D.﹣(﹣a+1)=a+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
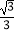 x﹣
x﹣ 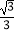 与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 .
与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 . 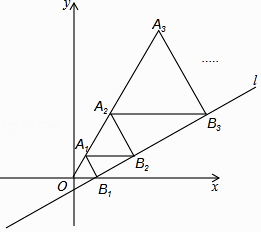
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的周长为16,面积为8
 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 . 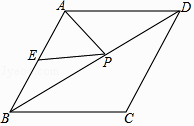
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+
x+  分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+  经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.

(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
相关试题

