Question

【题目】如图，一次函数y=kx+b的图象与坐标轴分别交于A、B两点，与反比例函数y= 的图象在第一象限的交点为C，CD⊥x轴，垂足为D，若OB=3，OD=6，△AOB的面积为3．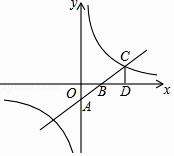
（1）求一次函数与反比例函数的解析式；
（2）直接写出当x＞0时，kx+b﹣ ＜0的解集．

Answer 1

【答案】
（1）解：∵S△AOB=3，OB=3，

∴OA=2，

∴B（3，0），A（0，﹣2），

代入y=kx+b得： ，

解得：k= ，b=﹣2，

∴一次函数y= x﹣2，

∵OD=6，

∴D（6，0），CD⊥x轴，

当x=6时，y= ×6﹣2=2

∴C（6，2），

∴n=6×2=12，

∴反比例函数的解析式是y= ；

（2）解：当x＞0时，kx+b﹣ ＜0的解集是0＜x＜6．
【解析】（1）根据三角形面积求出OA，得出A、B的坐标，代入一次函数的解析式即可求出解析式，把x=6代入求出D的坐标，把D的坐标代入反比例函数的解析式求出即可；（2）根据图象即可得出答案．