【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
参考答案:
【答案】
(1)
证明:∵△ABC是等腰三角形,且∠BAC=120°,
∴∠ABD=∠ACB=30°,
∴∠ABD=∠ADE=30°,
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB,
∴△ABD∽△DCE;
(2)
解:如图1,∵AB=AC=2,∠BAC=120°,
过A作AF⊥BC于F,

∴∠AFB=90°,
∵AB=2,∠ABF=30°,
∴AF= ![]() AB=1,
AB=1,
∴BF= ![]() ,
,
∴BC=2BF=2 ![]() ,
,
则DC=2 ![]() ﹣x,EC=2﹣y,
﹣x,EC=2﹣y,
∵△ABD∽△DCE,
∴ ![]() ,
,
∴ ![]() ,
,
化简得:y= ![]() x+2(0<x<2
x+2(0<x<2 ![]() );
);
(3)
解:当AD=DE时,如图2,

由(1)可知:此时△ABD∽△DCE,
则AB=CD,即2=2 ![]() ﹣x,
﹣x,
x=2 ![]() ﹣2,代入y=
﹣2,代入y= ![]() x+2,
x+2,
解得:y=4﹣2 ![]() ,即AE=4﹣2
,即AE=4﹣2 ![]() ,
,
当AE=ED时,如图3,

∠EAD=∠EDA=30°,∠AED=120°,
∴∠DEC=60°,∠EDC=90°,
则ED= ![]() EC,即y=
EC,即y= ![]() (2﹣y),
(2﹣y),
解得:y= ![]() ,即AE=
,即AE= ![]() ,
,
当AD=AE时,
∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在,
∴当△ADE是等腰三角形时,AE=4﹣2 ![]() 或
或 ![]() .
.
【解析】(1)根据两角相等证明:△ABD∽△DCE;(2)如图1,作高AF,根据直角三角形30°的性质求AF的长,根据勾股定理求BF的长,则可得BC的长,根据(1)中的相似列比例式可得函数关系式,并确定取值;(3)分三种情况进行讨论:①当AD=DE时,如图2,由(1)可知:此时△ABD∽△DCE,则AB=CD,即2=2 ![]() ﹣x;②当AE=ED时,如图3,则ED=
﹣x;②当AE=ED时,如图3,则ED= ![]() EC,即y=
EC,即y= ![]() (2﹣y);③当AD=AE时,∠AED=∠EDA=30°,∠EAD=120°,
(2﹣y);③当AD=AE时,∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在.
【考点精析】利用函数关系式和等腰三角形的性质对题目进行判断即可得到答案,需要熟知用来表示函数关系的数学式子叫做函数解析式或函数关系式;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
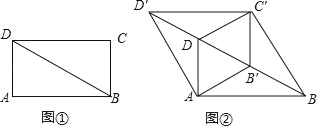
查看答案和解析>>【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为 ;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2+10x+9=0,配方后可得( )
A.(x+5)2=16
B.(x+5)2=1
C.(x+10)2=91
D.(x+10)2=109 -
科目: 来源: 题型:
查看答案和解析>>【题目】当a=0时,方程ax+b=0(其中x是未知数,b是已知数)的解的情况是( )
A. 唯一解B. 无解C. 有无数多个解D. 无解或有无数多个解
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5)
B.(﹣8,5)
C.(﹣8,﹣1)
D.(2,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A与∠B互余,∠B与∠C互补,若∠A=50°,则∠C的度数是( )
A.40° B.50° C.130° D.140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中不能用平方差公式计算的是( )
A. (x-y)(-x+y)B. (-x+y)(-x-y)C. (-x-y)(x-y)D. (x+y)(-x+y)
相关试题

