【题目】解一元二次不等式![]() .
.
请按照下面的步骤,完成本题的解答.
解:![]() 可化为
可化为![]() .
.
(1)依据“两数相乘,同号得正”,可得不等式组①![]() 或不等式组②________.
或不等式组②________.
(2)解不等式组①,得________.
(3)解不等式组②,得________.
(4)一元二次不等式![]() 的解集为________.
的解集为________.
参考答案:
【答案】 ![]()
![]()
![]()
![]() 或
或![]()
【解析】分析:(1)根据题干条件列出不等式组,进行解答.
(2)、(3)根据解不等式组的步骤进行求解即可;
(4)由(2)、(3)可得出不等式组的解集.
详解:∵![]() 可化为
可化为![]() .
.
∴依据“两数相乘,同号得正”,可得不等式组①![]() 或不等式组②
或不等式组②![]()
(2) ![]()
由①得,x>-2;
由②得,x>2;
所以,不等式组的解集为:x>2;
(3)![]()
由①得,x<-2;
由②得,x<2;
所以,不等式组的解集为:x<-2;
(4) 一元二次不等式![]() 的解集为:
的解集为: ![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.

注:水费按月结算,不足1立方米的不收费.若某户居民1月份用水8立方米,则应交水费:2×6+4×(8-6)=20(元).
(1)若该户居民2月份交水费16元,计算该户居民2月份的用水量;
(2)若该户居民3月份用水12.5立方米,则应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=
 x2﹣
x2﹣ x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
(1)求出点A,B,D的坐标;
(2)如图1,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′.首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
(3)如图2,若点M是抛物线上一点,点N在y轴上,连接CM、MN.当△CMN是以MN为直角边的等腰直角三角形时,直接写出点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在一条可以折叠的数轴上,点A,B分别表示数-9和4.
(1)A,B两点之间的距离为________.
(2)如图2,如果以点C为折点,将这条数轴向右对折,此时点A落在点B的右边1个单位长度处,则点C表示的数是________.
(3)如图1,若点A以每秒3个单位长度的速度沿数轴向右运动,点B以每秒2个单位长度的速度也沿数轴向右运动,那么经过多少时间,A、B两点相距4个单位长度?
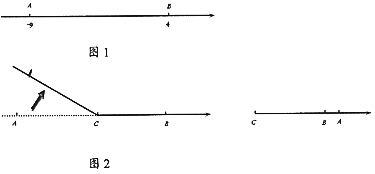
-
科目: 来源: 题型:
查看答案和解析>>【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度
 (单位:
(单位: )与足球被踢出后经过的时间
)与足球被踢出后经过的时间 (单位:
(单位: )之间的关系如下表:
)之间的关系如下表:
0
1
2
3
4
5
6
7
…

0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为
 ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线 ;③足球被踢出
;③足球被踢出 时落地;④足球被踢出
时落地;④足球被踢出 时,距离地面的高度是
时,距离地面的高度是 .
.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
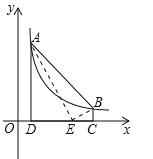
查看答案和解析>>【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.线段DC上有一点E,当△ABE的面积等于5时,点E的坐标为 .
相关试题

