搜索
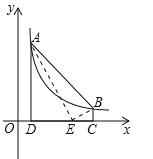
【题目】如图，点A（m，6），B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．线段DC上有一点E，当△ABE的面积等于5时，点E的坐标为 ．
参考答案：
【答案】（5，0）．
【解析】
试题分析：由题意得：
，解得：
，∴A（1，6），B（6，1），
设反比例函数解析式为y=
，将A（1，6）代入得：k=6，则反比例解析式为y=
；
设E（x，0），则DE=x﹣1，CE=6﹣x，∵AD⊥x轴，BC⊥x轴，∴∠ADE=∠BCE=90°，
连接AE，BE，则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE=
（BC+AD）DC﹣
DEAD﹣CEBC=×（1+6）×5﹣（x﹣1）×6﹣（6﹣x）×1=
﹣
x=5，解得：x=5，则E（5，0）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解一元二次不等式
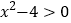．请按照下面的步骤，完成本题的解答．
解：
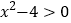可化为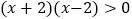
．（1）依据“两数相乘，同号得正”，可得不等式组①
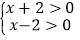或不等式组②________．（2）解不等式组①，得________．
（3）解不等式组②，得________．
（4）一元二次不等式
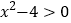的解集为________． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在一条可以折叠的数轴上，点A，B分别表示数-9和4.
(1)A，B两点之间的距离为________.
(2)如图2，如果以点C为折点，将这条数轴向右对折，此时点A落在点B的右边1个单位长度处，则点C表示的数是________.
(3)如图1，若点A以每秒3个单位长度的速度沿数轴向右运动，点B以每秒2个单位长度的速度也沿数轴向右运动，那么经过多少时间，A、B两点相距4个单位长度?
-
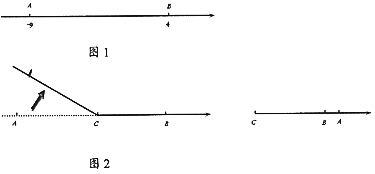
科目： 来源： 题型：
查看答案和解析>>【题目】足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度
（单位：
）与足球被踢出后经过的时间
（单位：
）之间的关系如下表：
0
1
2
3
4
5
6
7
…
0
8
14
18
20
20
18
14
…
下列结论：①足球距离地面的最大高度为
；②足球飞行路线的对称轴是直线
；③足球被踢出
时落地；④足球被踢出
时，距离地面的高度是
.其中正确结论的个数是（ ）
A．1 B．2 C．3 D．4
-
科目： 来源： 题型：
查看答案和解析>>【题目】一根长80厘米的弹簧，一端固定，如果另一端挂上物体，那么在正常情况下物体的质量每增加1千克可使弹簧增长2厘米。
（1）正常情况下，当挂着
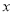千克的物体时，弹簧的长度
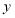是多少厘米？（2）正常情况下，当挂物体的质量为6千克时，弹簧的长度是多少厘米？
（3）正常情况下，当弹簧的长度是120厘米时，所挂物体的质量是多少千克？
（4）如果弹簧的长度超过了150厘米时，弹簧就失去弹性，问此弹簧能否挂质量为40千克的物体？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若
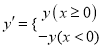，则称点Q为点P的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．
（1）若点（﹣1，﹣2）是一次函数
图象上点M的“可控变点”，则点M的坐标为 ；（2）若点P在函数
（
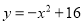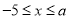）的图象上，其“可控变点”Q的纵坐标y′的取值范围是
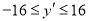，则实数a的取值范围是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】中国的茶文化源远流长，根据制作方法和茶多酚氧化（发酵）程度的不同，可分为六大类：绿茶（不发酵）、白茶（轻微发酵）、黄茶（轻发酵）、青茶（半发酵）、黑茶（后发酵）、红茶（全发酵）．春节将至，为款待亲朋好友，小叶去茶庄选购茶叶．茶庄有碧螺春、龙井两种绿茶，一种青茶——武夷岩茶及一种黄茶——银针出售．
（1）随机购买一种茶叶，是绿茶的概率为________；
（2）随机购买两种茶叶，求一种是绿茶、一种是银针的概率．
相关试题
