【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案:
【答案】解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
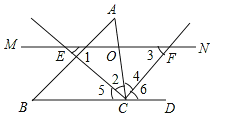
∴∠2=∠5,4=∠6。
∵MN∥BC,∴∠1=∠5,3=∠6。
∴∠1=∠2,∠3=∠4。∴EO=CO,FO=CO。
∴OE=OF。
(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°。
∵CE=12,CF=5,∴![]() 。
。
∴OC=![]() EF=6.5。
EF=6.5。
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形。理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形。
∵∠ECF=90°,∴平行四边形AECF是矩形。
【解析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案。
(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可根据直角三角形斜边上的中线性质得出CO的长。
(3)根据平行四边形的判定以及矩形的判定得出即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米
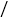 小时,如果再载了另一个人,则速度为20千米
小时,如果再载了另一个人,则速度为20千米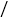 小时
小时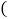 摩托车不允许带两个人,即每车至多载两人
摩托车不允许带两个人,即每车至多载两人 每个儿子如果步行速度为5千米
每个儿子如果步行速度为5千米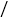 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为______小时.
小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为______小时. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OP为一条拉直的细线,长为7cm,A,B两点在OP上,若先握住点B,将OB折向BP,使得OB重叠在BP上,如图
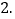 再从图2的A点及与A点重叠处一起剪开,使得细线分成三段
再从图2的A点及与A点重叠处一起剪开,使得细线分成三段 若这三段的长度由短到长之比为1:2:4,其中以点P为一端的那段细线最长,则OB的长为______cm.
若这三段的长度由短到长之比为1:2:4,其中以点P为一端的那段细线最长,则OB的长为______cm.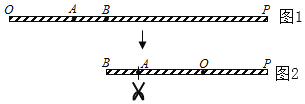
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是必然事件的是( )
A.任意画一个正五边形,它是中心对称图形
B.实数x使式子 有意义,则实数x>3
有意义,则实数x>3
C.a,b均为实数,若a=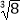 ,b=
,b= 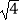 ,则a>b
,则a>b
D.5个数据分别是:6,6,3,2,1,则这组数据的中位数是3 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)先化简,再求值:( ﹣
﹣  )
)  ,其中x=
,其中x=  ﹣2.
﹣2.
(2)计算:|﹣4|+( )﹣2﹣(
)﹣2﹣(  ﹣1)0﹣
﹣1)0﹣ 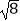 cos45°.
cos45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面上四点A,B,C,D,按下列要求画出图形;
(1)射线AB,直线CB;
(2)取线段AB的中点E,连接DE并延长与直线CB交于点O;
(3)在所画的图形中,若AB=6,BE=BC=
 OB,求OC的长.
OB,求OC的长.
相关试题

