【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
参考答案:
【答案】(1)当t=![]() 时,四边形ABQP是平行四边形(2)y=
时,四边形ABQP是平行四边形(2)y=![]() t+3(3)存在,当t=
t+3(3)存在,当t=![]() 时,点O在线段AP的垂直平分线上
时,点O在线段AP的垂直平分线上
【解析】
(1)根据ASA证明△APO≌△CQO,再根据全等三角形的性质得出AP=CQ=t,则BQ=5-t,再根据平行四边形的判定定理可知当AP∥BQ,AP=BQ时,四边形ABQP是平行四边形,即t=5-t,求出t的值即可求解;
(2)过A作AH⊥BC于点H,过O作OG⊥BC于点G,根据勾股定理求出AC=4,由Rt△ABC的面积计算可求得AH=![]() ,利用三角形中位线定理可得OG=
,利用三角形中位线定理可得OG=![]() ,再根据四边形OQCD的面积y= S△OCD+S△OCQ=
,再根据四边形OQCD的面积y= S△OCD+S△OCQ=![]() OC·CD+
OC·CD+![]() CQ·OG,代入数值计算即可得y与t之间的函数关系式;
CQ·OG,代入数值计算即可得y与t之间的函数关系式;
(3)如图2,若OE是AP的垂直平分线,可得AE=![]() AP=
AP=![]() ,∠AEO=90°,根据勾股定理可得AE2+OE2=AO2,由(2)知:AO=2,OE=
,∠AEO=90°,根据勾股定理可得AE2+OE2=AO2,由(2)知:AO=2,OE=![]() ,列出关于t的方程,解方程即可求出t的值.
,列出关于t的方程,解方程即可求出t的值.
(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠PAO=∠QCO.
又∵∠AOP=∠COQ,
∴△APO≌△CQO,
∴AP=CQ=t.
∵BC=5,
∴BQ=5-t.
∵AP∥BQ,
当AP=BQ时,四边形ABQP是平行四边形,
即t=5-t,∴t=![]() ,
,
∴当t=![]() 时,四边形ABQP是平行四边形;
时,四边形ABQP是平行四边形;
(2) 图1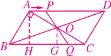
如图1,过A作AH⊥BC于点H,过O作OG⊥BC于点G.
在Rt△ABC中,∵AB=3,BC=5,∴AC=4,
∴CO=![]() AC=2,
AC=2,
S△ABC=![]() AB·AC=
AB·AC=![]() BC·AH,
BC·AH,
∴3×4=5AH,
∴AH=![]() .
.
∵AH∥OG,OA=OC,
∴GH=CG,
∴OG=![]() AH=
AH=![]() ,
,
∴y=S△OCD+S△OCQ=![]() OC·CD+
OC·CD+![]() CQ·OG,
CQ·OG,
∴y=![]() ×2×3+
×2×3+![]() ×t×
×t×![]() =
=![]() t+3;
t+3;
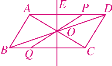 图2
图2
(3)存在.
如图2,∵OE是AP的垂直平分线,
∴AE=![]() AP=
AP=![]() ,∠AEO=90°,
,∠AEO=90°,
由(2)知:AO=2,OE=![]() ,
,
由勾股定理得:AE2+OE2=AO2,
∴(![]() t)2+(
t)2+(![]() )2=22,
)2=22,
∴t=![]() 或-
或-![]() (舍去),
(舍去),
∴当t=![]() 时,点O在线段AP的垂直平分线上.
时,点O在线段AP的垂直平分线上.
故答案为:(1)当t=![]() 时,四边形ABQP是平行四边形(2)y=
时,四边形ABQP是平行四边形(2)y=![]() t+3(3)存在,当t=
t+3(3)存在,当t=![]() 时,点O在线段AP的垂直平分线上.
时,点O在线段AP的垂直平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 交
交 轴于点
轴于点 、点
、点 ,交
,交 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.(1)求
 两点的坐标;
两点的坐标;(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点
 异于
异于 ,且
,且 在对称轴右侧),直线
在对称轴右侧),直线 交对称轴于N,
交对称轴于N,直线BE交对称轴于
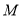 ,对称轴交
,对称轴交 轴于
轴于 ,试确定
,试确定 、
、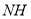 的数量关系并说明理由.
的数量关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,A(-1,5)、B(-1,0),C(-4,3).
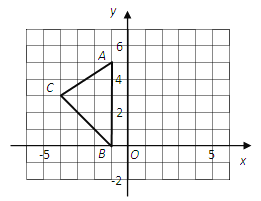
(1)△ABC的面积是 .
(2)在下图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.
(3)写出点A1、B1、C1的坐标.
-
科目: 来源: 题型:
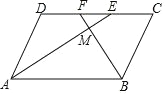
查看答案和解析>>【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
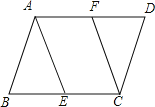
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为促进课堂教学,提高教学质量,对本校七年级学生进行了一次“你最喜欢的课堂教学 方式”的问卷调查.根据收回的问卷,学校绘制了“频率分布表”和“频数分布条形图”.请你根据图表中提供 的信息,解答下列问题:
代
号
教学方式
最喜欢频
数
频
率
1
老师讲,学生听
20
0.10
2
老师提出问题,学生探索思考
100
3
学生自行阅读教材,独立思考
30
0.15
4
分组讨论,解决问题
0.25

(1)补全“频率分布表”;
(2)在“频数分布条形图”中,将代号为4的部分补充完整;
(3)你最喜欢以上哪种教学方式或另外的教学方式,请提出你的建议,并简要说理由.
-
科目: 来源: 题型:
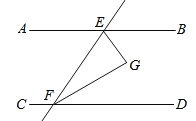
查看答案和解析>>【题目】如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,
(1)若∠AEF=50°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
相关试题

