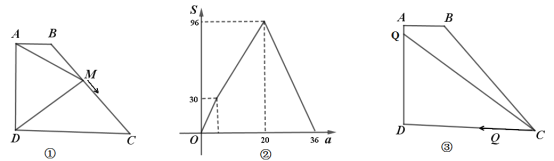
【题目】如图①,四边形![]() 中,
中,![]() .
.
(1)动点![]() 从
从![]() 出发,以每秒1个单位的速度沿路线
出发,以每秒1个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() 关于
关于![]() 的函数图象如图②所示,求
的函数图象如图②所示,求![]() 的长.
的长.
(2)如图③动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿路线
出发,以每秒2个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,同时,动点
停止,同时,动点![]() 从点
从点![]() 出发,以每秒5个单位的速度沿路线
出发,以每秒5个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,当
,当![]() 点运动到
点运动到![]() 边上时,连接
边上时,连接![]() ,当
,当![]() 的面积为8时,求
的面积为8时,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() .
.
【解析】
(1)根据题意由函数图象可知动点![]() 从
从![]() 出发,以每秒1个单位的速度从C到D耗时16秒求出CD,再利用三角形面积公式求得AD即可;
出发,以每秒1个单位的速度从C到D耗时16秒求出CD,再利用三角形面积公式求得AD即可;
(2)由题意可知只能有P和![]() 点都在
点都在![]() 边上,此时分当P在Q上方时以及当P在Q下方时两种情况运用数形结合思维进行分析得出答案.
边上,此时分当P在Q上方时以及当P在Q下方时两种情况运用数形结合思维进行分析得出答案.
解:(1)由函数图象可知动点![]() 从
从![]() 出发,以每秒1个单位的速度从C到D耗时36-20=16秒,即CD=16,而此时
出发,以每秒1个单位的速度从C到D耗时36-20=16秒,即CD=16,而此时![]() 的面积为96,又因为
的面积为96,又因为![]() ,
,
即有![]() ,解得
,解得![]() .
.
所以![]() .
.
(2)由题意可知Q运动到点![]() 停止的时间为
停止的时间为![]() ,而P运动到点
,而P运动到点![]() 停止的时间为6,
停止的时间为6,
所以只能有P和![]() 点都在
点都在![]() 边上,此时以PQ为底边,CD为高,
边上,此时以PQ为底边,CD为高,
设运动时间为![]() ,则AP=2t,QD=5t-16,(
,则AP=2t,QD=5t-16,(![]() ),
),
①当P在Q上方时,则有PQ=AD-AP-QD= ![]() ,
,
可知![]() 的面积为8时即
的面积为8时即![]() ,解得
,解得![]() (满足条件);
(满足条件);
②当P在Q下方时,则有PQ=QD-(AD-AP)= ![]() ,
,
可知![]() 的面积为8时即
的面积为8时即![]() ,解得
,解得![]() (满足条件).
(满足条件).
所以当![]() 的面积为8时,
的面积为8时,![]() 的值为
的值为![]() 和
和![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计费;月用水量超过20m3时,超过部分按2.6元/m3计费.设每户家庭的月用水量为xm3时,应交水费y元.
(1)试求出0≤x≤20和x>20时,y与x之间的函数关系;
(2)小明家第二季度用水量的情况如下:月份
四月
五月
六月
用水量(m3)
15
17
21
小明家这个季度共缴纳水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中
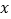 表示时间,
表示时间, 表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )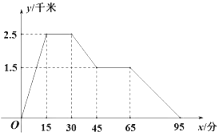
A. 体育场离小敏家2.5千米B. 体育场离早餐店4千米
C. 小敏在体育场锻炼了15分钟D. 小敏从早餐店回到家用时30分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一组平行线
 过点A作AM⊥
过点A作AM⊥ 于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线
于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线 于点C,在直线
于点C,在直线 上取点B使BM=CN,若直线
上取点B使BM=CN,若直线 与
与 间的距离为2,
间的距离为2, 与
与 间的距离为4,则BC=______.
间的距离为4,则BC=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板如图摆放,∠OAB=∠OCD=90°,∠AOB=60°,∠COD=45°,OM平分∠AOD,ON平分∠COB,则∠MON的度数为( )
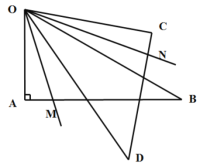
A.60°B.45°C.65.5°D.52.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
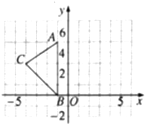
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
-
科目: 来源: 题型:
查看答案和解析>>【题目】无锡市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°.B灯先转动2秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是______秒.
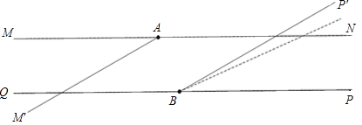
相关试题

