【题目】某城市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计费;月用水量超过20m3时,超过部分按2.6元/m3计费.设每户家庭的月用水量为xm3时,应交水费y元.
(1)试求出0≤x≤20和x>20时,y与x之间的函数关系;
(2)小明家第二季度用水量的情况如下:
月份 | 四月 | 五月 | 六月 |
用水量(m3) | 15 | 17 | 21 |
小明家这个季度共缴纳水费多少元?
参考答案:
【答案】
(1)解:因为月用水量不超过20m3时,按2元/m3计费,所以当0≤x≤20时,y与x的函数表达式是y=2x;
因为月用水量超过20m3时,其中的20m3仍按2元/m3收费,超过部分按2.6元/m3计费,所以当x>20时,y与x的函数表达式是y=2×20+2.6(x﹣20),
即y=2.6x﹣12;
综上所述,y= ![]()
(2)解:因为小明家四、五月份的用水都不超过20m3,六月份的用水超过20m3,
所以把x=15代入2x中,得2×15=30(元);
把17代入2x中,得2×17=34(元);
把x=21代入2.6x﹣12中,得2.6×21﹣12=42.6(元).
∴小花家这个季度共缴纳水费:30+34+42.6=106.6(元).
答:小花家这个季度共缴纳水费1066元
【解析】因为月用水量不超过20m3时,按2元/m3计费,所以当0≤x≤20时,y与x的函数表达式是y=2x;因为月用水量超过20m3时,其中的20m3仍按2元/m3收费,超过部分按2.6元/m3计费,所以当x>20时,y与x的函数表达式是y=2×20+2.6(x﹣20);(2)因为小明家四、五月份的用水都不超过20m3,六月份的用水超过20m3,分别代入解析式,求出结果即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图1,AC和BD相交于点O,OA=OC,OB=OD,求证:DC∥AB.
(2)如图2,在⊙O中,直径AB=6,AB与弦CD相交于点E,连接AC、BD,若AC=2,求cosD的值.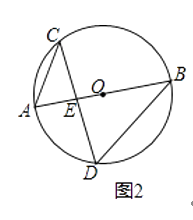
-
科目: 来源: 题型:
查看答案和解析>>【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计),第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车,小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林,离入口处的路程
 (米)与时间
(米)与时间 (分)的函数关系如图2所示.
(分)的函数关系如图2所示.(1)求第一班车从入口处到达塔林的时间.
(2)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变).
(3)若小聪在8:30至8:50之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过3分钟的概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:①若
 则
则 ②若
②若 则
则 ③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中
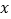 表示时间,
表示时间, 表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )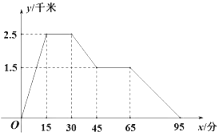
A. 体育场离小敏家2.5千米B. 体育场离早餐店4千米
C. 小敏在体育场锻炼了15分钟D. 小敏从早餐店回到家用时30分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一组平行线
 过点A作AM⊥
过点A作AM⊥ 于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线
于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线 于点C,在直线
于点C,在直线 上取点B使BM=CN,若直线
上取点B使BM=CN,若直线 与
与 间的距离为2,
间的距离为2, 与
与 间的距离为4,则BC=______.
间的距离为4,则BC=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形
 中,
中,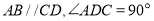 .
.(1)动点
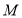 从
从 出发,以每秒1个单位的速度沿路线
出发,以每秒1个单位的速度沿路线 运动到点
运动到点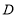 停止,设运动时间为
停止,设运动时间为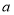 ,
,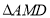 的面积为
的面积为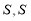 关于
关于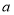 的函数图象如图②所示,求
的函数图象如图②所示,求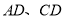 的长.
的长.(2)如图③动点
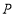 从点
从点 出发,以每秒2个单位的速度沿路线
出发,以每秒2个单位的速度沿路线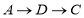 运动到点
运动到点 停止,同时,动点
停止,同时,动点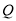 从点
从点 出发,以每秒5个单位的速度沿路线
出发,以每秒5个单位的速度沿路线 运动到点
运动到点 停止,设运动时间为
停止,设运动时间为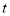 ,当
,当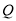 点运动到
点运动到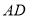 边上时,连接
边上时,连接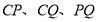 ,当
,当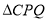 的面积为8时,求
的面积为8时,求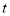 的值.
的值.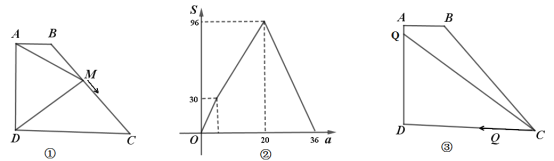
相关试题

