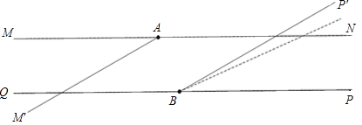
【题目】无锡市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°.B灯先转动2秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是______秒.
参考答案:
【答案】![]() 或
或![]()
【解析】
设A灯旋转时间为t秒,B灯光束第一次到达BQ需要180÷10=18秒,推出t≤18-2,即t≤16秒,利用平行线的判定,构建方程解决问题即可.
设A灯旋转时间为t秒,B灯光束第一次到达BQ要180÷10=18秒,t≤18-2,即t≤16,由题意,满足以下条件时,两灯的光束能互相平①如图1,
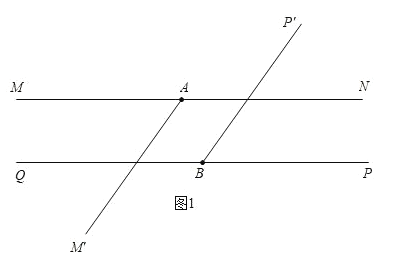
![]() ,30t=10(2+t);解得t=1,
,30t=10(2+t);解得t=1,
②如图2,
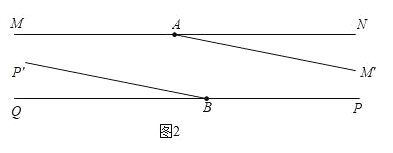
![]() ,30t-180+10(2+t)=180,解得t=
,30t-180+10(2+t)=180,解得t=![]() ;
;
综上所述,满足条件的t值为1秒或者![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形
 中,
中,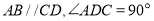 .
.(1)动点
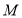 从
从 出发,以每秒1个单位的速度沿路线
出发,以每秒1个单位的速度沿路线 运动到点
运动到点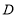 停止,设运动时间为
停止,设运动时间为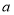 ,
,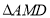 的面积为
的面积为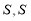 关于
关于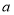 的函数图象如图②所示,求
的函数图象如图②所示,求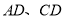 的长.
的长.(2)如图③动点
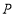 从点
从点 出发,以每秒2个单位的速度沿路线
出发,以每秒2个单位的速度沿路线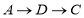 运动到点
运动到点 停止,同时,动点
停止,同时,动点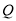 从点
从点 出发,以每秒5个单位的速度沿路线
出发,以每秒5个单位的速度沿路线 运动到点
运动到点 停止,设运动时间为
停止,设运动时间为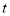 ,当
,当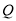 点运动到
点运动到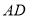 边上时,连接
边上时,连接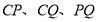 ,当
,当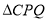 的面积为8时,求
的面积为8时,求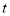 的值.
的值.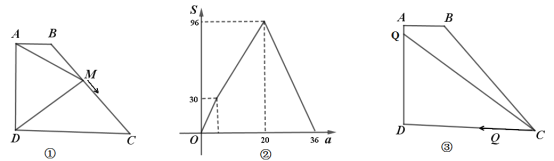
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板如图摆放,∠OAB=∠OCD=90°,∠AOB=60°,∠COD=45°,OM平分∠AOD,ON平分∠COB,则∠MON的度数为( )
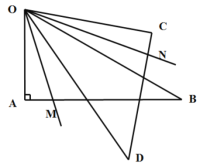
A.60°B.45°C.65.5°D.52.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
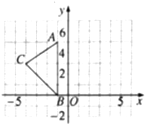
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
-
科目: 来源: 题型:
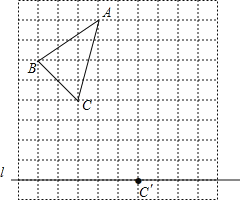
查看答案和解析>>【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△
 ,点C的对应点是直线上的格点
,点C的对应点是直线上的格点 .
.
(1)画出△
 .
.(2)若连接
 、
、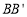 ,则这两条线段之间的关系是 .
,则这两条线段之间的关系是 .(3)试在直线
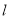 上画出所有符合题意的格点P,使得由点
上画出所有符合题意的格点P,使得由点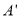 、
、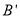 、
、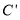 、P四点围成的四边形的面积为9.
、P四点围成的四边形的面积为9. -
科目: 来源: 题型:
查看答案和解析>>【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.(友情提醒:翻折前后的两个三角形的对应边相等,对应角相等.)



(1)如图①,当AE⊥BC时,求证:DE∥AC.
(2)若
 ,∠BAD=x° .
,∠BAD=x° .①如图②,当DE⊥BC时,求x的值;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
相关试题

