【题目】学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人.
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调m人去两处支援,其中![]() ,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
参考答案:
【答案】(1)应从乙处调7人去甲处;(2)当m=92时: 则应调往甲处各86人,乙处6人
当m=96时: 则应调往甲处各89人,乙处7人
【解析】
(1)设应从乙处调x人到甲处,则乙处剩下(96-x)人,根据甲处植树的人数是乙处植树人数的3倍得出方程,求出x的值;
(2)设调往甲处y人,甲处现有(220+y)人,则调往乙处(m-y)人,乙处现有(96+m-y)人,此时甲处植树的人数是乙处植树人数的3倍,由此可得方程:![]() .解此方程后即得调往乙处的人数,进而求出调往甲处多少人.
.解此方程后即得调往乙处的人数,进而求出调往甲处多少人.
解:(1)设应从乙处调x人到甲处,则乙处剩下(96-x)人,
列方程得:![]()
解得:x=17
(2)设调往甲处y人,甲处现有(220+y)人,则调往乙处(m-y)人,乙处现有(96+m-y)人,由此可得方程:![]()
∴![]()
∴![]()
∵![]() ,y<m,m,y均为整数
,y<m,m,y均为整数
当m=91时:![]() (舍去)
(舍去)
当m=92时:![]()
当m=93时:![]() (舍去)
(舍去)
当m=94时:![]() (舍去)
(舍去)
当m=95时:![]() (舍去)
(舍去)
当m=96时:![]()
当m=97时:![]() (舍去)
(舍去)
当m=98时:![]() (舍去)
(舍去)
当m=99时:![]() (舍去)
(舍去)
综上所述:当m=92时: 则应调往甲处各86人,乙处6人
当m=96时: 则应调往甲处各89人,乙处7人
答:(1)应从乙处调7人去甲处;(2)当m=92时: 则应调往甲处各86人,乙处6人
当m=96时: 则应调往甲处各89人,乙处7人
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
 为二次函数
为二次函数 图象的顶点,直线
图象的顶点,直线 分别交
分别交 轴正半轴,
轴正半轴, 轴于点
轴于点 ,
, .
.
(1)判断顶点
 是否在直线
是否在直线 上,并说明理由.
上,并说明理由.(2)如图1,若二次函数图象也经过点
 ,
, ,且
,且 ,根据图象,写出
,根据图象,写出 的取值范围.
的取值范围.(3)如图2,点
 坐标为
坐标为 ,点
,点 在
在 内,若点
内,若点 ,
, 都在二次函数图象上,试比较
都在二次函数图象上,试比较 与
与 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
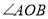 是一钢架,且
是一钢架,且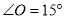 ,为使钢架更加牢固,需在其内部添加-一些钢管
,为使钢架更加牢固,需在其内部添加-一些钢管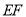 、
、 、
、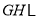 ,添加的钢管都与
,添加的钢管都与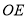 相等,则最多能添加这样的钢管( )
相等,则最多能添加这样的钢管( )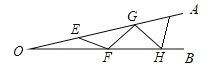
A.
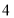 根B.
根B.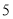 根C.
根C.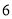 根D.无数根
根D.无数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
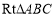 中,
中,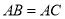 ,
,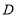 、
、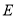 是斜边
是斜边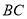 上两点,且
上两点,且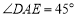 ,将
,将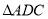 绕
绕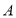 顺时针旋转
顺时针旋转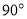 后,得到
后,得到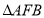 ,连接
,连接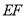 ,则下列结论不正确的是( )
,则下列结论不正确的是( )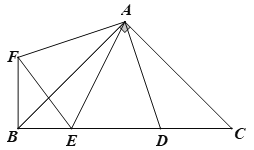
A.
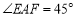 B.
B.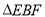 为等腰直角三角形
为等腰直角三角形C.
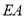 平分
平分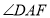 D.
D.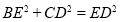
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”。
(1)概念理解:
如图1,在
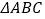 中,
中,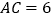 ,
,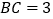 .
.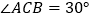 ,试判断
,试判断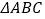 是否是“等高底”三角形,请说明理由.
是否是“等高底”三角形,请说明理由.(2)问题探究:
如图2,
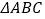 是“等高底”三角形,
是“等高底”三角形,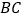 是“等底”,作
是“等底”,作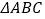 关于
关于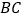 所在直线的对称图形得到
所在直线的对称图形得到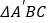 ,连结
,连结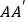 交直线
交直线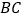 于点
于点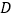 .若点
.若点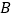 是
是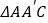 的重心,求
的重心,求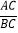 的值.
的值.(3)应用拓展:
如图3,已知
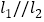 ,
,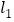 与
与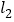 之间的距离为2.“等高底”
之间的距离为2.“等高底”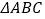 的“等底”
的“等底” 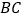 在直线
在直线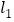 上,点
上,点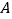 在直线
在直线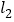 上
上,有一边的长是 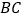 的
的 倍.将
倍.将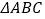 绕点
绕点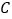 按顺时针方向旋转
按顺时针方向旋转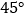 得到
得到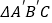 ,
,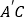 所在直线交
所在直线交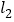 于点
于点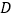 .求
.求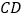 的值.
的值.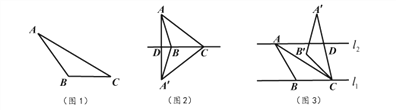
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
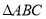 在平面直角坐标系内,顶点的坐标分别为
在平面直角坐标系内,顶点的坐标分别为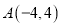 ,
,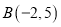 、
、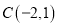 .
.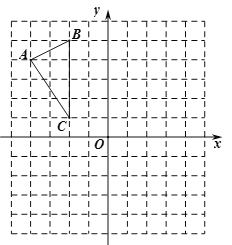
(1)平移
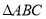 ,使点
,使点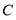 移到点
移到点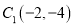 ,画出平移后的
,画出平移后的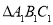 ,并写出点
,并写出点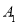 的坐标.
的坐标.(2)将
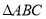 绕点
绕点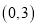 旋转
旋转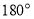 ,得到
,得到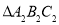 ,画出旋转后的
,画出旋转后的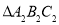 ,并写出点
,并写出点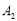 的坐标.
的坐标.(3)求(2)中的点
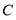 旋转到点
旋转到点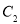 时,点
时,点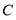 经过的路径长(结果保留
经过的路径长(结果保留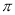 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )

A. 9 B. 10 C. 11 D. 12
相关试题

