【题目】如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )

A. 9 B. 10 C. 11 D. 12
参考答案:
【答案】D
【解析】
根据主视图以及俯视图,可得出最左边共有3行,根据俯视图可得出该几何体最左边由3列组成,故可得出小正方体最多块数.
解:综合主视图和俯视图,该几何体的底面最多应该有3+2=5个小正方体,
第二层最多有3个小正方体,第三层最多有3个小正方体,
因此组成这个几何体的小正方体最多块数是5+3+3=11个.
故答案为C.
本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人.
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调m人去两处支援,其中
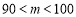 ,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”。
(1)概念理解:
如图1,在
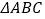 中,
中,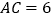 ,
,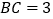 .
.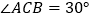 ,试判断
,试判断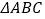 是否是“等高底”三角形,请说明理由.
是否是“等高底”三角形,请说明理由.(2)问题探究:
如图2,
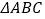 是“等高底”三角形,
是“等高底”三角形,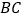 是“等底”,作
是“等底”,作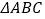 关于
关于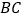 所在直线的对称图形得到
所在直线的对称图形得到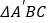 ,连结
,连结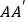 交直线
交直线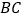 于点
于点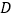 .若点
.若点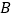 是
是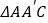 的重心,求
的重心,求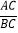 的值.
的值.(3)应用拓展:
如图3,已知
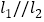 ,
,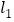 与
与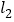 之间的距离为2.“等高底”
之间的距离为2.“等高底”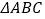 的“等底”
的“等底” 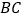 在直线
在直线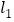 上,点
上,点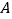 在直线
在直线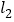 上
上,有一边的长是 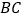 的
的 倍.将
倍.将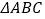 绕点
绕点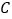 按顺时针方向旋转
按顺时针方向旋转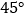 得到
得到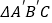 ,
,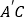 所在直线交
所在直线交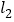 于点
于点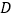 .求
.求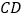 的值.
的值.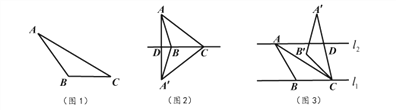
-
科目: 来源: 题型:
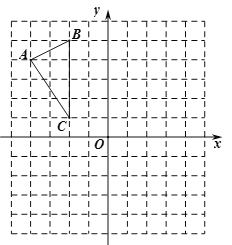
查看答案和解析>>【题目】如图,
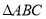 在平面直角坐标系内,顶点的坐标分别为
在平面直角坐标系内,顶点的坐标分别为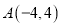 ,
,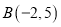 、
、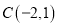 .
.
(1)平移
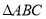 ,使点
,使点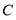 移到点
移到点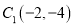 ,画出平移后的
,画出平移后的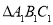 ,并写出点
,并写出点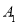 的坐标.
的坐标.(2)将
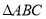 绕点
绕点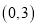 旋转
旋转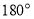 ,得到
,得到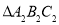 ,画出旋转后的
,画出旋转后的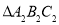 ,并写出点
,并写出点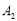 的坐标.
的坐标.(3)求(2)中的点
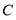 旋转到点
旋转到点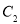 时,点
时,点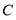 经过的路径长(结果保留
经过的路径长(结果保留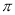 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB与直线CD相交于点O,OE平分
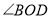 .
.
(1)如图①,若
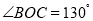 ,求
,求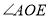 的度数;
的度数;(2)如图②,射线OF在
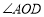 内部.
内部.①若
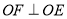 ,判断OF是否为
,判断OF是否为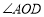 的平分线,并说明理由;
的平分线,并说明理由;②若OF平分
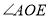 ,
,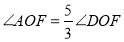 ,求
,求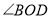 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义,如果一个四边形有一条对角线能将其分成一个等边三角形和一个直角三角形,那么这个四边形叫做等垂四边形,这条对角线叫做这个四边形的等垂对角线.
(1)已知
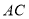 是四边形
是四边形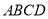 的等垂对角线,
的等垂对角线,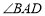 ,
,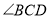 均为钝角,且
均为钝角,且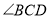 比
比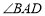 大
大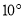 ,那么
,那么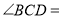 ________.
________.(2)如图,已知
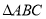 与
与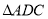 关于直线
关于直线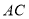 对称,
对称,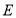 、
、 两点分别在
两点分别在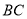 、
、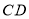 边上,
边上, ,
,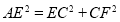 ,
, .求证:四边形
.求证:四边形 是等垂四边形。
是等垂四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

相关试题

