【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.

(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
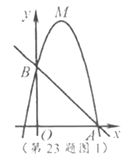
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
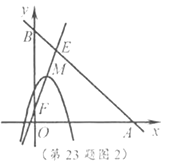
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
参考答案:
【答案】(1)点![]() 在直线
在直线![]() 上,理由见解析;(2)
上,理由见解析;(2)![]() 的取值范围为
的取值范围为![]() 或
或![]() .(3)①当
.(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.
【解析】(1)写出点![]() 的坐标,代入直线
的坐标,代入直线![]() 进行判断即可.
进行判断即可.
(2)直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,求出点
,求出点![]() 坐标,把
坐标,把![]() 在抛物线上,代入求得
在抛物线上,代入求得![]() ,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出
,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出![]() 时,
时,![]() 的取值范围.
的取值范围.
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,而直线
,而直线![]() 表达式为
表达式为![]() ,联立方程组
,联立方程组![]() ,得
,得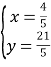 .点
.点![]() ,
,![]() .分三种情况进行讨论.
.分三种情况进行讨论.
【解答】
(1)∵点![]() 坐标是
坐标是![]() ,
,
∴把![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
(2)如图1,∵直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,∴点
,∴点![]() 坐标为
坐标为![]() .
.
又∵![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ,
,
∴当![]() 时,得
时,得![]() ,
,![]() ,∴
,∴![]() .
.
观察图象可得,当![]() 时,
时,
![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
(3)如图2,∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
而直线![]() 表达式为
表达式为![]() ,
,
解方程组![]() ,得
,得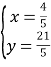 .∴点
.∴点![]() ,
,![]() .
.
∵点![]() 在
在![]() 内,
内,
∴![]() .
.
当点![]() ,
,![]() 关于抛物线对称轴(直线
关于抛物线对称轴(直线![]() )对称时,
)对称时,
![]() ,∴
,∴![]() .
.
且二次函数图象的开口向下,顶点![]() 在直线
在直线![]() 上,
上,
综上:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,滑动调节式遮阳伞的立柱
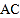 垂直于地面
垂直于地面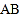 ,
,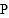 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为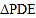 ,
,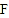 为
为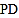 中点,
中点,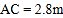 ,
,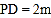 ,
,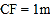 ,
,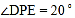 .当点
.当点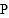 位于初始位置
位于初始位置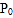 时,点
时,点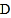 与
与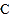 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与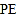 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.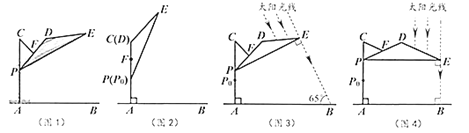
(1)上午10:00时,太阳光线与地面的夹角为
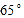 (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点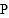 需从
需从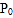 上调多少距离?(结果精确到
上调多少距离?(结果精确到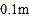 )
)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点
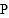 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到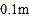 )
)(参考数据:
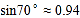 ,
,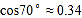 ,
,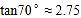 ,
,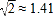 ,
,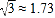 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,求
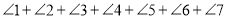 的度数.
的度数.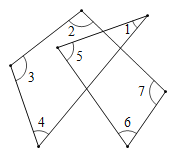
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
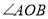 是一钢架,且
是一钢架,且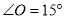 ,为使钢架更加牢固,需在其内部添加-一些钢管
,为使钢架更加牢固,需在其内部添加-一些钢管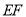 、
、 、
、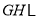 ,添加的钢管都与
,添加的钢管都与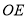 相等,则最多能添加这样的钢管( )
相等,则最多能添加这样的钢管( )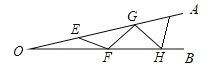
A.
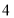 根B.
根B.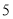 根C.
根C.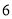 根D.无数根
根D.无数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
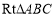 中,
中,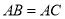 ,
,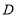 、
、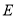 是斜边
是斜边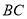 上两点,且
上两点,且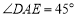 ,将
,将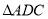 绕
绕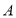 顺时针旋转
顺时针旋转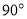 后,得到
后,得到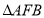 ,连接
,连接 ,则下列结论不正确的是( )
,则下列结论不正确的是( )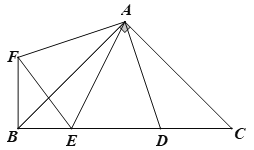
A.
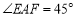 B.
B.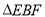 为等腰直角三角形
为等腰直角三角形C.
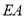 平分
平分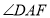 D.
D.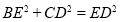
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人.
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调m人去两处支援,其中
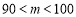 ,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
相关试题

