【题目】如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E。
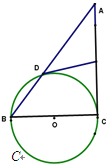
(1)求证:AC是⊙O的切线;
(2)若AD:DB=3:2,AC=15,求⊙O的直径。
参考答案:
【答案】(1)连接OD、CD,先根据切线的性质得到OD⊥DE,即∠1+∠2=90°,再根据圆周角定理可得∠BDC=90°,再结合E为AC的中点,根据直角三角形的性质可得DE=CE=AE=![]() AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;(2)
AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;(2)![]()
【解析】
试题分析:(1)连接OD、CD,先根据切线的性质得到OD⊥DE,即∠1+∠2=90°,再根据圆周角定理可得∠BDC=90°,再结合E为AC的中点,根据直角三角形的性质可得DE=CE=AE=![]() AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;
AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;
(2)分别证得△ACD∽△ABC与△ACD∽△BCD,根据相似三角形的性质可得![]() ,
,![]() ,由AD:DB=3:2可设AD=3k,DB=2k,则AB=5k,即可求得结果.
,由AD:DB=3:2可设AD=3k,DB=2k,则AB=5k,即可求得结果.
(1)连接OD、CD
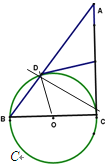
∵DE是⊙O的切线,切点为D
∴OD⊥DE于D
∴∠ODE=90°,即∠1+∠2=90°;
∵BC为⊙O的直径
∴∠BDC=90°
∴∠ADC=90°
∵E为AC的中点
∴DE=CE=AE=![]() AC
AC
∴∠2=∠3
∵⊙O中,OC=OD
∴∠1=∠4
∴∠3+∠4=∠1+∠2=90°
∴OC⊥AC于C
∴AC是⊙O的切线;
(2)∵∠ACD=∠BDC=90°,∠A=∠A
∴△ACD∽△ABC
同理:△ACD∽△BCD
∴![]() ①
①
![]() ②
②
∵AD:DB=3:2
∴设AD=3k,DB=2k,则AB=5k
∴①![]()
![]()
![]()
②![]()
![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,试问
,试问 与
与 平行吗?为什么?
平行吗?为什么?下面是说明
 的过程,请在( )内写上理由.
的过程,请在( )内写上理由.
解:
 ,
, ( )
( ) ( )
( )又
 ,
, (等量代换)
(等量代换) ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级甲、乙两班在参加全校演讲比赛的预选赛中,每班前
 名的成绩分别为:
名的成绩分别为:甲班:
 ,
, ,
,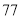 ,
,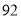 ,
, ;乙班:
;乙班: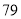 ,
, ,
,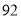 ,
, ,
,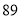 ;通过数据分析,列表如下:
;通过数据分析,列表如下:班级
平均分
中位数
众数
方差
甲

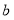
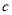
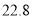
乙
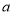


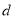
(1)直接写出表中
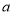 ,
,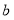 ,
,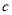 的值;
的值;(2)求
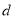 的值,你认为哪个班前
的值,你认为哪个班前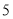 名同学的成绩较好?说明理由.
名同学的成绩较好?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有3个小球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个小球是白球的概率;
(2)摸出1个小球,记下颜色后放回,并搅均,再摸出1个小球.求两次摸出的小球恰好颜色不同的概率.(要求画树状图或列表)
-
科目: 来源: 题型:
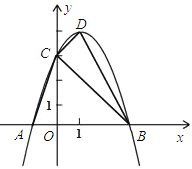
查看答案和解析>>【题目】如图,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0)和B,与y轴交于点C(0,3).
(1)求此抛物线的解析式及点B的坐标;
(2)设抛物线的顶点为D,连接CD、DB、CB、AC.
①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;
-
科目: 来源: 题型:
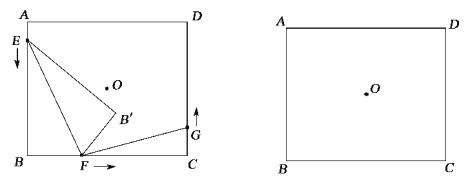
查看答案和解析>>【题目】如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为xcm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
(1)当t= s时,四边形EBFB'为正方形;
(2)当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?
(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
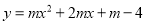 (
(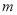 是常数,
是常数, 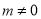 ).
).(
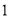 )当该函数的图像与
)当该函数的图像与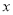 轴没有交点时,求
轴没有交点时,求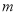 的取值范围.
的取值范围.(
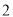 )把该函数的图像沿
)把该函数的图像沿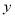 轴向上平移多少个单位长度后,得到的函数的图像与
轴向上平移多少个单位长度后,得到的函数的图像与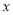 轴只有一个公共点?
轴只有一个公共点?
相关试题

