【题目】一个不透明的布袋里装有3个小球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个小球是白球的概率;
(2)摸出1个小球,记下颜色后放回,并搅均,再摸出1个小球.求两次摸出的小球恰好颜色不同的概率.(要求画树状图或列表)
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .见解析
.见解析
【解析】
试题分析:(1)由一个不透明的布袋里装有3个小球,其中2个红球,1个白球,利用概率公式求解即可求得答案;
(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与两次摸出的小球恰好颜色不同的情况,再利用概率公式求解即可求得答案.
解:(1)∵一个不透明的布袋里装有3个小球,其中2个红球,1个白球,
∴P(摸出1个小球是白球)=![]() ;
;
(2)列表得:
红1 | 红2 | 白 | |
红1 | (红1,红1) | (红1,红2) | (红1,白) |
红2 | (红2,红1) | (红2,红2) | (红2,白) |
白 | (白,红1) | (白,红2) | (白,白) |
∵所有等可能情况一共有9种,其中颜色恰好不同有4种,
∴P(两次摸出的小球恰好颜色不同)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )
A.0.25×10-5 B.0.25×10-6 C.2.5×10-5 D.2.5×10-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0有两个根是x1,x2,那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+2x﹣5=0,求(x1+2)(x2+2)和(
 +
+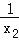 )的值;
)的值;(2)已知a,b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求
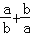 的值.
的值. -
科目: 来源: 题型:
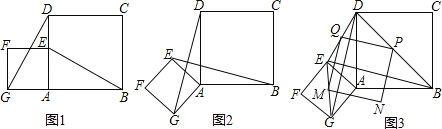
查看答案和解析>>【题目】如图1所示,四边形AEFG与四边形ABCD是正方形,其中G、A、B三点在同一直线上.连接DG、BE.完成下面问题:
(1)求证:BE=DG;
(2)如图2,将正方形AEFG绕点A逆时针转过一定角度时,小明发现:BE=DG且BE⊥DG,请你帮助小明证明这两个结论;
(3)如图3,小明还发现:在旋转过程中,分别连接EG、GB、BD、DE的中点,得到的四边形MNPQ是正方形.若AB=a,AE=b其中a>b,你能帮小明求出正方形MNPQ的面积的范围吗?写出过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”为[1,m-3]的一次函数是正比例函数,则关于x的方程mx-6=0的解为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个人患了流感,经过两轮传染后共有121人患了流感;因此一个人传染了 个人,三轮共有 人患了流感.(期间无人治愈)
-
科目: 来源: 题型:
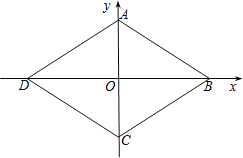
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的四个顶点均在坐标轴上,A(0,2),∠ABC=60°.把一条长为2013个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在菱形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A.(

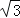 ,
, ) B.(
) B.(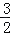
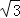 ,﹣
,﹣ ) C.(﹣
) C.(﹣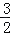
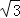 ,
, ) D.(﹣
) D.(﹣ ,
,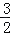
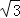 )
)
相关试题

