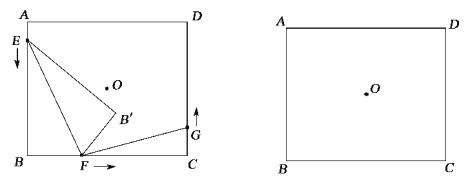
【题目】如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为xcm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
(1)当t= s时,四边形EBFB'为正方形;
(2)当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?
(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)2.5;(2)3或4;(3)不存在,理由见解析
【解析】
(1)利用正方形的性质,得到BE=BF,列一元一次方程求解即可;
(2)分两种情况讨论,①△EBF≌△FCG,②△EBF≌△GCF,分别根据对应边相等列等式计算即可;
(3)本问为存在型问题.假设存在,则可以分别求出在同一条件下的t值,但它们互相矛盾,所以不存在.
解:(1)若四边形EBFB′为正方形,则BE=BF,BE=10-t,BF=3t,
即:10-t=3t,
解得t=2.5;
(2)分两种情况讨论:
①△EBF≌△FCG,
则EB=FC,BF=CG,
∴![]() ,
,
解得:![]() ,
,
②当△EBF≌△GCF时,
则EB=GC,BF=FC,
∴![]() ,
,
解得:![]() ,
,
综上,当x=3或4时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等;
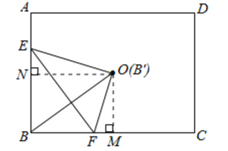
(3)假设存在实数t,使得点B′与点O重合.
如图,过点O作OM⊥BC于点M, ON⊥AB于点N,
则在Rt△OFM中![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]()
在Rt△OEN中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴假设不成立,
即不存在实数t,使得点B'与点O重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有3个小球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个小球是白球的概率;
(2)摸出1个小球,记下颜色后放回,并搅均,再摸出1个小球.求两次摸出的小球恰好颜色不同的概率.(要求画树状图或列表)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E。
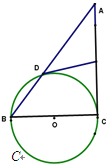
(1)求证:AC是⊙O的切线;
(2)若AD:DB=3:2,AC=15,求⊙O的直径。
-
科目: 来源: 题型:
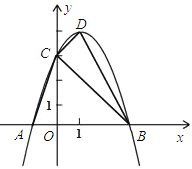
查看答案和解析>>【题目】如图,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0)和B,与y轴交于点C(0,3).
(1)求此抛物线的解析式及点B的坐标;
(2)设抛物线的顶点为D,连接CD、DB、CB、AC.
①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
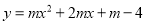 (
(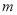 是常数,
是常数, 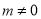 ).
).(
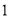 )当该函数的图像与
)当该函数的图像与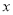 轴没有交点时,求
轴没有交点时,求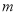 的取值范围.
的取值范围.(
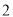 )把该函数的图像沿
)把该函数的图像沿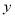 轴向上平移多少个单位长度后,得到的函数的图像与
轴向上平移多少个单位长度后,得到的函数的图像与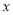 轴只有一个公共点?
轴只有一个公共点? -
科目: 来源: 题型:
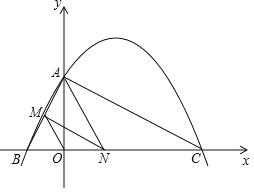
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校
 名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于
名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于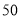 分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中
分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中 名学生的成绩(成绩取
名学生的成绩(成绩取 整数,总分
整数,总分 分)作为样本进行整理,得到下列不完整的统计图表:
分)作为样本进行整理,得到下列不完整的统计图表:

请根据所给信息,解答下列问题:
(1)
 ,
, ;
;(2)请补全频数分布直方图;
(3)若成绩在
 以上(包括
以上(包括 分)的为“优”等,则该校参加这次比赛的
分)的为“优”等,则该校参加这次比赛的 名学生中成绩“优”等约有多少人?
名学生中成绩“优”等约有多少人?
相关试题

