【题目】将正整数按如图的规律排列:平移表中的方框,方框中的4个数的和可能是( )
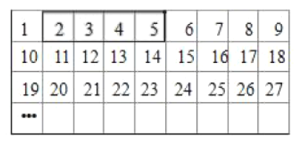
A.2010B.2014C.2018D.2020
参考答案:
【答案】A
【解析】
先根据表格中正整数的排列找出,方框中4个数变化规律的一般表达式(含n),再找出其在所有可能的平移方式下,这4个数的和,然后根据表达式中n的整数性求解即可.
随着方框向下平移,可表示出这4个数其变化规律的表达式为:![]()
将这4个数相加得:![]() (n为非负整数)
(n为非负整数)
这4个数向下平移后,可以有以下5中平移方式:
(1)向左移一个格
此时,这4个数相加得:![]()
(2)向右移一个格
此时,这4个数相加得:![]()
(3)向右移二个格
此时,这4个数相加得:![]()
(4)向右移三个格
此时,这4个数相加得:![]()
(5)向右移四个格
此时,这4个数相加得:![]()
将四个选项分别代入上述6个代数式,经计算,只有A选项代入![]() 时,解出的n为整数,即当
时,解出的n为整数,即当![]() 时,有
时,有![]()
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
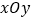 中,以直线
中,以直线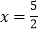 为对称轴的抛物线
为对称轴的抛物线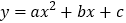 与直线
与直线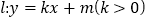 交于
交于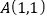 ,
,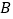 两点,与
两点,与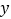 轴交于
轴交于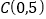 ,直线
,直线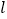 与
与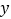 轴交于点
轴交于点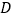 .
.(1)求抛物线的函数表达式;
(2)设直线
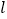 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为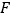 ,
,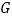 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若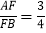 ,且
,且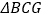 与
与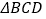 的面积相等,求点
的面积相等,求点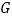 的坐标;
的坐标;(3)若在
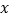 轴上有且只有一点
轴上有且只有一点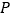 ,使
,使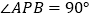 ,求
,求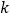 的值.
的值.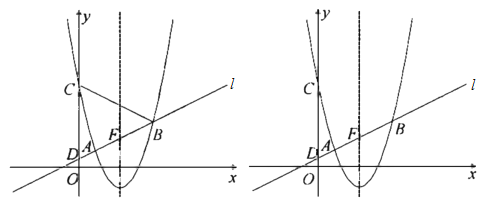
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
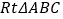 中,
中,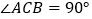 ,
,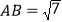 ,
,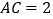 ,过点
,过点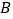 作直线
作直线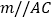 ,将
,将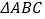 绕点
绕点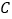 顺时针得到
顺时针得到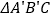 (点
(点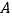 ,
,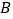 的对应点分别为
的对应点分别为 ,
,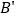 ),射线
),射线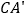 ,
,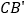 分别交直线
分别交直线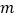 于点
于点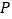 ,
,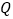 .
. 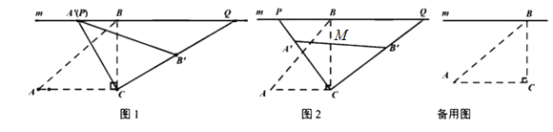 (1)如图1,当
(1)如图1,当 与
与 重合时,求
重合时,求 的度数;
的度数;(2)如图2,设
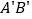 与
与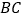 的交点为
的交点为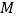 ,当
,当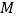 为
为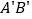 的中点时,求线段
的中点时,求线段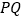 的长;
的长;(3)在旋转过程时,当点
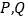 分别在
分别在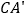 ,
,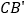 的延长线上时,试探究四边形
的延长线上时,试探究四边形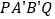 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形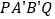 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中,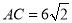 ,
,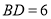 ,
,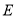 是
是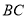 边的中点,
边的中点,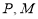 分别是
分别是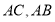 上的动点,连接
上的动点,连接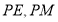 ,则
,则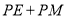 的最小值是( )
的最小值是( )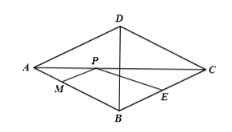
A. 6B.
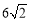 C.
C. 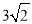 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用
 (元)与种植面积
(元)与种植面积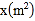 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当
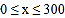 和
和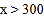 时,
时, 与
与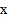 的函数关系式;
的函数关系式;(2)广场上甲、乙两种花卉的种植面积共
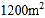 ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于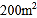 ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元? -
科目: 来源: 题型:
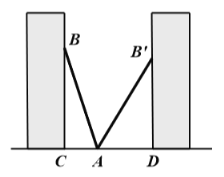
查看答案和解析>>【题目】如图,小巷左右两侧是竖直的墙,一架梯子
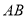 斜靠在左墙时,梯子底端到左墙角的距离
斜靠在左墙时,梯子底端到左墙角的距离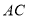 为0.7米,顶端到地面距离
为0.7米,顶端到地面距离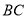 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离
为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离 为2米,求小巷的宽度
为2米,求小巷的宽度 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
相关试题

