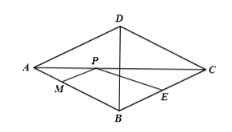
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点,
边的中点,![]() 分别是
分别是![]() 上的动点,连接
上的动点,连接![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A. 6B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
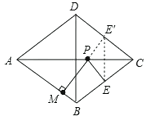
作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,点P、M即为使PE+PM取得最小值的点,由PE+PM=PE′+PM=E′M利用S菱形ABCD=![]() ACBD=ABE′M求解可得答案.
ACBD=ABE′M求解可得答案.
解:如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,则此时点P、M使PE+PM取得最小值的,
其PE+PM=PE′+PM=E′M,
∵四边形ABCD是菱形,
∴点E′在CD上,
∵![]() ,BD=6,
,BD=6,
∴AB=![]() ,
,
由S菱形ABCD=![]() ACBD=ABE′M得
ACBD=ABE′M得![]() ×
×![]() ×6=
×6=![]() E′M,
E′M,
解得:E′M=![]() ,
,
即PE+PM的最小值是![]() ,
,
故选:D.
-
科目: 来源: 题型:
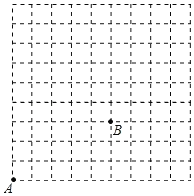
查看答案和解析>>【题目】如图,在9×9的方格(每小格边长为1个单位)中,有格点A,B现点A沿网格线跳动规定:向右跳动一格需要m秒,向上跳动一格需要n秒,且每次跳动后均落在格点上.
(1)点A跳到点B,需要 秒(用含m,n的代数式表示).
(2)已知m=1,n=2.
①若点A向右跳动3秒,向上跳动10秒到达点C,请在图中标出点C的位置,并求出以BC为边的正方形的面积.
②若点A跳动5秒到达点D,请直接写出点D与点B之间距离的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,以直线
中,以直线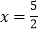 为对称轴的抛物线
为对称轴的抛物线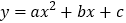 与直线
与直线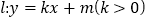 交于
交于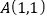 ,
,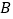 两点,与
两点,与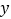 轴交于
轴交于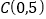 ,直线
,直线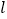 与
与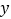 轴交于点
轴交于点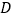 .
.(1)求抛物线的函数表达式;
(2)设直线
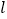 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为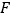 ,
,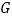 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若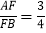 ,且
,且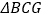 与
与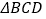 的面积相等,求点
的面积相等,求点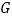 的坐标;
的坐标;(3)若在
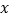 轴上有且只有一点
轴上有且只有一点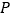 ,使
,使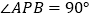 ,求
,求 的值.
的值.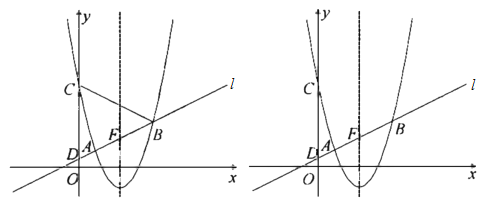
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
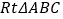 中,
中,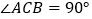 ,
,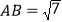 ,
,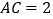 ,过点
,过点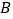 作直线
作直线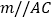 ,将
,将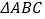 绕点
绕点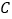 顺时针得到
顺时针得到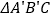 (点
(点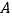 ,
,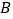 的对应点分别为
的对应点分别为 ,
,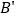 ),射线
),射线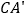 ,
,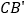 分别交直线
分别交直线 于点
于点 ,
, .
. 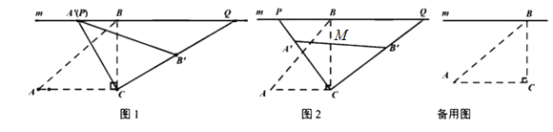 (1)如图1,当
(1)如图1,当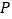 与
与 重合时,求
重合时,求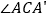 的度数;
的度数;(2)如图2,设
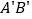 与
与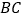 的交点为
的交点为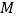 ,当
,当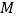 为
为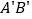 的中点时,求线段
的中点时,求线段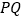 的长;
的长;(3)在旋转过程时,当点
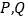 分别在
分别在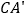 ,
,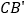 的延长线上时,试探究四边形
的延长线上时,试探究四边形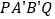 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形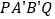 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数按如图的规律排列:平移表中的方框,方框中的4个数的和可能是( )
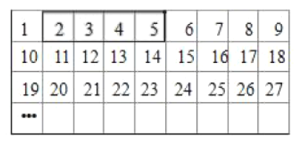
A.2010B.2014C.2018D.2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用
 (元)与种植面积
(元)与种植面积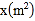 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当
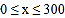 和
和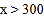 时,
时, 与
与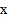 的函数关系式;
的函数关系式;(2)广场上甲、乙两种花卉的种植面积共
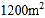 ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于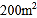 ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元? -
科目: 来源: 题型:
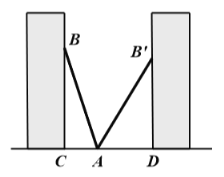
查看答案和解析>>【题目】如图,小巷左右两侧是竖直的墙,一架梯子
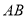 斜靠在左墙时,梯子底端到左墙角的距离
斜靠在左墙时,梯子底端到左墙角的距离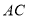 为0.7米,顶端到地面距离
为0.7米,顶端到地面距离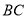 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离
为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离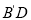 为2米,求小巷的宽度
为2米,求小巷的宽度 .
.
相关试题

