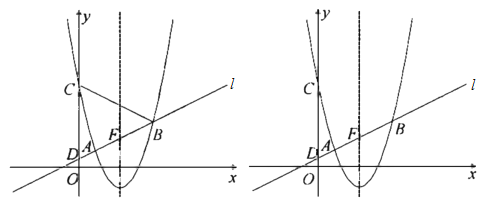
【题目】如图,在平面直角坐标系![]() 中,以直线
中,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)设直线![]() 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为![]() ,
,![]() 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若![]() ,且
,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
(3)若在![]() 轴上有且只有一点
轴上有且只有一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() .;(2)点
.;(2)点![]() 坐标为
坐标为![]() ;
;![]() .(3)
.(3)![]() .
.
【解析】(1)根据已知列出方程组求解即可;
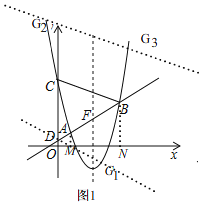
(2)作AM⊥x轴,BN⊥x轴,垂足分别为M,N,求出直线l的解析式,再分两种情况分别求出G点坐标即可;
(3)根据题意分析得出以AB为直径的圆与x轴只有一个交点,且P为切点,P为MN的中点,运用三角形相似建立等量关系列出方程求解即可.
(1)由题可得: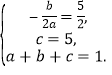 解得
解得![]() ,
,![]() ,
,![]() .
.
![]() 二次函数解析式为:
二次函数解析式为:![]() .
.
(2)作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() ,
,
 ,解得
,解得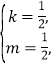 ,
,![]() ,
,![]() .
.
同理,![]() .
.
![]() ,
,
![]() ①
①![]() (
(![]() 在
在![]() 下方),
下方),![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
②![]() 在
在![]() 上方时,直线
上方时,直线![]() 与
与![]() 关于
关于![]() 对称.
对称.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
综上所述,点![]() 坐标为
坐标为![]() ;
;![]() .
.
(3)由题意可得:![]() .
.
![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
![]() ,
,![]() ,
,![]() .
.
设![]() 的中点为
的中点为![]() ,
,
![]() 点有且只有一个,
点有且只有一个,![]() 以
以![]() 为直径的圆与
为直径的圆与![]() 轴只有一个交点,且
轴只有一个交点,且![]() 为切点.
为切点.
![]() 轴,
轴,![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达
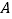 处时,测得小岛
处时,测得小岛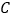 位于它的北偏东
位于它的北偏东 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛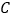 位于它的北偏东
位于它的北偏东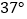 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛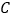 的正南方向的
的正南方向的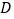 处,求还需航行的距离
处,求还需航行的距离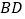 的长.
的长.(参考数据:
 ,
,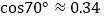 ,
,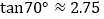 ,
,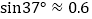 ,
,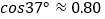 ,
,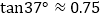 )
)
-
科目: 来源: 题型:
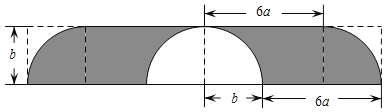
查看答案和解析>>【题目】国庆期间,广场上设置了一个庆祝国庆70周年的造型(如图所示).造型平面呈轴对称,其正中间为一个半径为b的半圆,摆放花草,其余部分为展板.求:
(1)展板的面积是 .(用含a,b的代数式表示)
(2)若a=0.5米,b=2米,求展板的面积.
(3)在(2)的条件下,已知摆放花草部分造价为450元/平方米,展板部分造价为80元/平方米,求制作整个造型的造价(π取3).
-
科目: 来源: 题型:
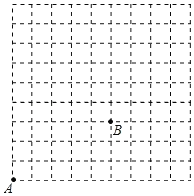
查看答案和解析>>【题目】如图,在9×9的方格(每小格边长为1个单位)中,有格点A,B现点A沿网格线跳动规定:向右跳动一格需要m秒,向上跳动一格需要n秒,且每次跳动后均落在格点上.
(1)点A跳到点B,需要 秒(用含m,n的代数式表示).
(2)已知m=1,n=2.
①若点A向右跳动3秒,向上跳动10秒到达点C,请在图中标出点C的位置,并求出以BC为边的正方形的面积.
②若点A跳动5秒到达点D,请直接写出点D与点B之间距离的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
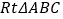 中,
中,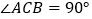 ,
,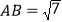 ,
,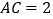 ,过点
,过点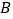 作直线
作直线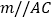 ,将
,将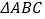 绕点
绕点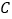 顺时针得到
顺时针得到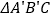 (点
(点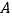 ,
,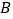 的对应点分别为
的对应点分别为 ,
,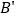 ),射线
),射线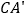 ,
,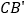 分别交直线
分别交直线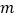 于点
于点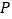 ,
,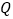 .
. 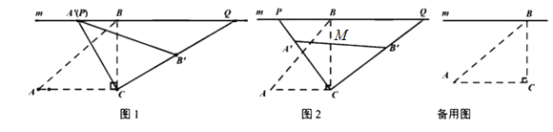 (1)如图1,当
(1)如图1,当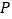 与
与 重合时,求
重合时,求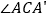 的度数;
的度数;(2)如图2,设
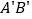 与
与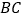 的交点为
的交点为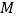 ,当
,当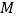 为
为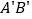 的中点时,求线段
的中点时,求线段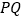 的长;
的长;(3)在旋转过程时,当点
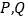 分别在
分别在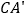 ,
,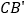 的延长线上时,试探究四边形
的延长线上时,试探究四边形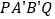 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形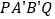 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
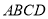 中,
中,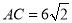 ,
,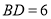 ,
,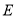 是
是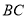 边的中点,
边的中点,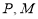 分别是
分别是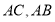 上的动点,连接
上的动点,连接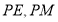 ,则
,则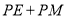 的最小值是( )
的最小值是( )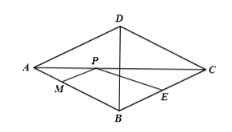
A. 6B.
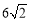 C.
C. 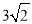 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数按如图的规律排列:平移表中的方框,方框中的4个数的和可能是( )
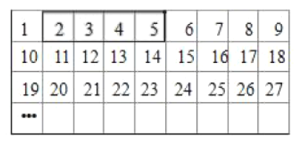
A.2010B.2014C.2018D.2020
相关试题

