【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
参考答案:
【答案】(1)![]() ;(2)应分配甲种花卉种植面积为
;(2)应分配甲种花卉种植面积为![]() ,乙种花卉种植面积为
,乙种花卉种植面积为![]() ,才能使种植总费用最少,最少总费用为119000元.
,才能使种植总费用最少,最少总费用为119000元.
【解析】(1)由图可知y与x的函数关系式是分段函数,待定系数法求解析式即可.
(2)设甲种花卉种植为 a m2,则乙种花卉种植(12000-a)m2,根据实际意义可以确定a的范围,结合种植费用y(元)与种植面积x(m2)之间的函数关系可以分类讨论最少费用为多少.
(1)![]()
(2)设甲种花卉种植面积为![]() ,则乙种花卉种植面积为
,则乙种花卉种植面积为![]() .
.
![]()
![]() .
.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 元.
元.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 元.
元.
![]() ,
,![]() 当
当![]() 时,总费用最低,最低为119000元.
时,总费用最低,最低为119000元.
此时乙种花卉种植面积为![]() .
.
答:应分配甲种花卉种植面积为![]() ,乙种花卉种植面积为
,乙种花卉种植面积为![]() ,才能使种植总费用最少,最少总费用为119000元.
,才能使种植总费用最少,最少总费用为119000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的三点A、B、C分别表示有理数a、b、c,且|a|>|c|>|b|.
(1)化简|a+c|﹣2|c﹣b|;
(2)若b的倒数是它本身,且AB:BO:OC=6:2:3,求(1)中代数式的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
次数,1, 2, 3, 4, 5, 6
甲:79,78,84,81,83,75
乙:83,77,80,85,80,75
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数.
(2)写出甲、乙测验成绩的中位数.
(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某县结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见下表
一户居民一个月用电量的范围
电费价格(单位:元/千瓦时)
不超过150千瓦时的部分
a
超过150千瓦时,但不超过230千瓦时的部分
b
超过230千瓦时的部分
a+0.33
2019年10月份,该县居民甲用电100千瓦时,交费64元;居民乙用电200千瓦时,交费134.5元.
(1)根据题意,求出上表中a和b的值;
(2)实行“阶梯电价”收费以后,该县居民当月用电多少千瓦时时,其当月的平均电价为0.67元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P(m,n)是抛物线y=
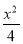 -1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
-1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.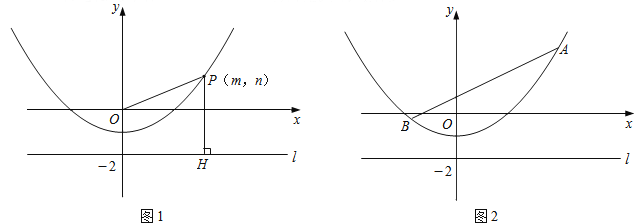
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线y=
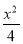 -1上滑动,求A,B两点到直线l的距离之和的最小值.
-1上滑动,求A,B两点到直线l的距离之和的最小值. -
科目: 来源: 题型:
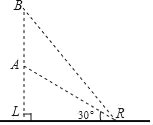
查看答案和解析>>【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.
相关试题

