【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
参考答案:
【答案】(1)16,17;(2)14;(3)2800.
【解析】
(1)将数据按照大小顺序重新排列,计算出中间两个数的平均数即是中位数,出现次数最多的即为众数;
(2)根据平均数的概念,将所有数的和除以10即可;
(3)用样本平均数估算总体的平均数.
(1)按照大小顺序重新排列后,第5、第6个数分别是15和17,所以中位数是(15+17)÷2=16,17出现3次最多,所以众数是17,
故答案为:16,17;
(2)![]() 14,
14,
答:这10位居民一周内使用共享单车的平均次数是14次;
(3)200×14=2800
答:该小区居民一周内使用共享单车的总次数为2800次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=a
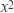 +bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
A. abc<0 B. 2a+b<0 C. a-b+c<0 D. 4ac-b2<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1, 将Cl绕点B中心对称变换得C2, C2与x轴交于另一点C,将C2绕点C中心对称变换得C3, 连接C与C3的顶点,则图中阴影部分的面积为( )
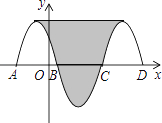
A. 32 B. 24 C. 36 D. 48
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=
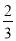 x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣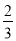 )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )
A. 大于0 B. 等于0 C. 小于0 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线
 ,且
,且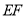 和
和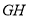 之间的距离为
之间的距离为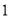 ,小明同学制作了一个直角三角形硬纸板
,小明同学制作了一个直角三角形硬纸板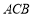 ,其中
,其中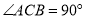 ,
, ,
,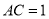 .小明利用这块三角板进行了如下的操作探究:
.小明利用这块三角板进行了如下的操作探究: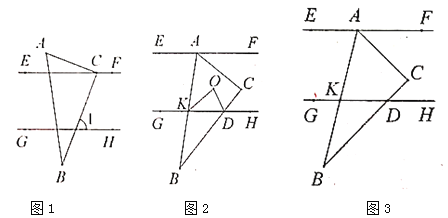
(1)如图1,若点
 在直线
在直线 上,且
上,且 .求
.求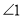 的度数;
的度数;(2)若点
 在直线
在直线 上,点
上,点 在
在 和
和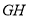 之间(不含
之间(不含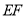 、
、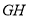 上),边
上),边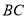 、
、 与直线
与直线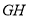 分别交于点
分别交于点 和点
和点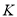 .
.①如图2,
 、
、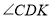 的平分线交于点
的平分线交于点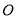 .在
.在 绕着点
绕着点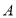 旋转的过程中,
旋转的过程中, 的度数是否变化?若不变,求出
的度数是否变化?若不变,求出 的度数;若变化,请说明理由;
的度数;若变化,请说明理由;②如图3,在
 绕着点
绕着点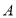 旋转的过程中,设
旋转的过程中,设 ,
,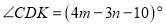 ,求
,求 的取值范
的取值范 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的中线BD,CE交于点O,F,G分别是BO,CO的中点.
的中线BD,CE交于点O,F,G分别是BO,CO的中点.(1)求证:四边形DEFG是平行四边形;
(2)若AB=AC,则四边形DEFG是 (填写特殊的平行四边形);
(3)当四边形DEFG为边长为2的正方形时,
 的周长为 .
的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
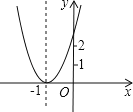
A.1 B.2 C.3 D.4
相关试题

