【题目】如图,在Rt△ABC中,∠C= ![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.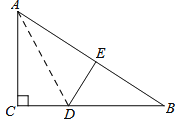
(1)问:△BDE与△BAC相似吗?
(2)已知AC=6,BC=8,求线段AD的长度.
参考答案:
【答案】
(1)
解答:相似.理由如下:
∵∠C= ![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,
∴∠C=∠AED= ![]() ,
,
∴∠DEB=∠C= ![]() ,
,
∵∠B=∠B,
∴△BDE∽△BAC;
(2)
解答:由勾股定理,得
AB= ![]() =10.
=10.
由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C= ![]() .
.
∴BE=AB-AE=10-6=4,
在Rt△BDE中,由勾股定理得,
![]() ,
,
即 ![]() ,
,
解得:CD=3,
在Rt△ACD中,由勾股定理得 ![]()
即 ![]() ,
,
解得:AD=3
【解析】根据折叠的性质得出∠C=∠AED= ![]() ,利用∠DEB=∠C , ∠B=∠B证明三角形相似;先由勾股定理求出AB的长,再由折叠的性质知DE=CD , AE=AC , BE=AB-AE , 在Rt△BDE中运用勾股定理求出DE , 即CD , 最后在Rt△ACD中运用勾股定理得出AD .
,利用∠DEB=∠C , ∠B=∠B证明三角形相似;先由勾股定理求出AB的长,再由折叠的性质知DE=CD , AE=AC , BE=AB-AE , 在Rt△BDE中运用勾股定理求出DE , 即CD , 最后在Rt△ACD中运用勾股定理得出AD .
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC , EF∥AB , 且S△ADE=4,S△EFC=9,则△ABC的面积为。
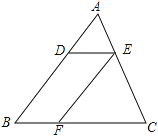
-
科目: 来源: 题型:
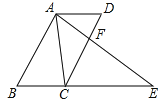
查看答案和解析>>【题目】如图,ABCD是平行四边形,点E在边BC延长线上,连AE交CD于点F , 如果∠EAC=∠D , 试问:ACBE与AECD是否相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某赛季中国职业篮球联赛第11轮前四名球队积分榜如下:
队名
比赛场次
胜场
负场
积分
辽宁
11
11
0
22
北京
11
10
1
21
广厦
11
9
2
20
新疆
11
8
3
19
(1)若一个队胜m场,则总积分为_____;
(2)某队的胜场总积分能否等于它的负场总积分,你的观点是:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣
 ;
;②由5=2﹣x移项得x=5﹣2;
③由
 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有一个两层楼的餐厅,甲、乙、丙三名学生各自随机选择其中的某个楼层的餐厅用餐,则甲、乙、丙三名学生在同一个楼层餐厅用餐的概率为()
A.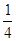
B.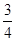
C.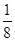
D.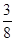
相关试题

