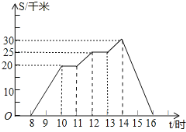
【题目】周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离s(千米)与时间t(时)之间的关系可以用图中的折线表示.现有如下信息:
①小李到达离家最远的地方是14时;
②小李第一次休息时间是10时;
③11时到12时,小李骑了5千米;
④返回时,小李的平均速度是10千米/时.
其中,正确的有( )
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
(1)从图象上可以知道,小亮到达离家最远的地方是在14时,最远距离是30千米;
(2)在图象开始处于水平状态的时刻就是小亮第一次休息的时刻;
(3)在这段时刻,我们看纵坐标时,两点对应的路程差即是小亮骑车的路程;
(4)由图形可知,回去时小亮是匀速行驶,中间没有休息,故速度是路程除以所用的时间.
(1)由图象知,在图形的最高点就是小亮到达离家最远30千米的地方.此时对应的时刻是14时.正确;
(2)休息的时候路程为0,即开始出现的第一个水平状态的时刻,由图象可知,小亮第一次休息的时刻是在10时.正确;
(3)由图象知,在这段时间内,小亮只在11时到12时运动,对应的路程差为5km.正确;
(4)返回时,小亮为匀速运动,路程为30千米,所用时间是2小时,故速度为15千米/小时.错误.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,张老师说:“
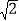 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把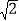 的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(
的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(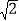 ﹣1)表示它的小数部分.”张老师说:“晶晶同学的说法是正确的,因为1<2<4,所以1<
﹣1)表示它的小数部分.”张老师说:“晶晶同学的说法是正确的,因为1<2<4,所以1<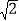 <2,所以
<2,所以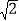 的整数部分是1,将这个数减去其整数部分,差就是小数部分.”亮亮说:“既然如此,因为2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.”亮亮说:“既然如此,因为2<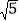 <3,所以
<3,所以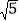 的小数部分就是(
的小数部分就是(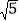 ﹣2)了.”张老师说:“亮亮真的很聪明.”接着,张老师出示了一道练习题:“已知8+
﹣2)了.”张老师说:“亮亮真的很聪明.”接着,张老师出示了一道练习题:“已知8+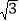 =x+y,其中x是一个整数,且0<y<1,请你求出2x+(
=x+y,其中x是一个整数,且0<y<1,请你求出2x+(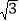 ﹣y)2019的值”.请同样聪明的你给出正确答案.
﹣y)2019的值”.请同样聪明的你给出正确答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

-
科目: 来源: 题型:
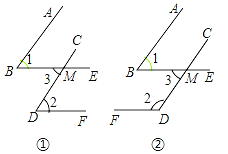
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=
 计算.解答下列问题:
计算.解答下列问题:
(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
(3)已知点A(5,5),B(-4,7),点P在x轴上,且要使PA+PB的和最小,求PA+PB的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AC、BD交于点O,点P、E分别是直线BD、BC上的动点,且PE=PC,过点E作EF∥AC交直线BD于点F.


(1)如图1,当∠COD=90°时,判断△BEF的形状,并说明理由;
(2)如图2,当点P在线段BO上时,求证:OP=BF;
(3)当∠COD=60°,CD=3时,请直接写出当△PEF成为直角三角形时的面积.
相关试题

