【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)BC=2CD,理由见解析.
【解析】
(1)利用矩形的性质,即可判定△FAE≌△CDE,即可得到CD=FA,再根据CD∥AF,即可得出四边形ACDF是平行四边形;
(2)先判定△CDE是等腰直角三角形,可得CD=DE,再根据E是AD的中点,可得AD=2CD,依据AD=BC,即可得到BC=2CD.
(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAE=∠CDE,
∵E是AD的中点,
∴AE=DE,
又∵∠FEA=∠CED,
∴△FAE≌△CDE,
∴CD=FA,
又∵CD∥AF,
∴四边形ACDF是平行四边形;
(2)BC=2CD.
证明:∵CF平分∠BCD,
∴∠DCE=45°,
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,
∴AD=2CD,
∵AD=BC,
∴BC=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b与y=kbx,它们在同一坐标系内的图象可能为 ( )
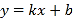
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
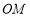 是
是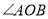 的平分线,点
的平分线,点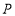 是射线
是射线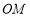 上一点,点C、D分别在射线
上一点,点C、D分别在射线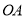 、
、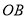 上,连接PC、PD.
上,连接PC、PD.(1)发现问题
如图①,当
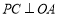 ,
,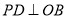 时,则PC与PD的数量关系是________.
时,则PC与PD的数量关系是________.(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当
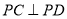 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
时,PC与PD在(1)中的数量关系还成立吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式组
 有且只有三个整数解,且关于x的分式方程
有且只有三个整数解,且关于x的分式方程  ﹣
﹣  =﹣1有整数解,则满足条件的整数a的值为( )
=﹣1有整数解,则满足条件的整数a的值为( )
A.15
B.3
C.﹣1
D.﹣15 -
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有五个小球,每个小球上面分别标着1,2,3,4,5这五个数字中的一个,这些小球除标的数字不同以外,其余的全部相同.把分别标有数字4、5的两个小球放入不透明的口袋 A 中,把分别标有数字1、2、3的三个小球放入不透明的口袋 B 中.现随机从 A 和 B 两个口袋中各取出一个小球,把从 A 口袋中取出的小球上标的数字记作 m,从 B 口袋中取出的小球上标的数字记作n,且m﹣n=k,则关于x的一元二次方程2x2﹣4x+k=0有解的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 是
是 的直角三角形,
的直角三角形, 的中点分别是点
的中点分别是点 点
点 ,动点
,动点 从点
从点 出发,按箭头方向通过
出发,按箭头方向通过 到
到 ;以
;以 的速度运动,设
的速度运动,设 点从
点从 开始运动的距离为
开始运动的距离为 ,
, 的面积为
的面积为 试回答以下问题:
试回答以下问题:(1)
 点从
点从 出发到
出发到 停止,写出
停止,写出 与
与 的函数关系式并写出
的函数关系式并写出 的取值范围.
的取值范围.(2)求出
 点从
点从 出发后几秒时,
出发后几秒时,

相关试题

