【题目】如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
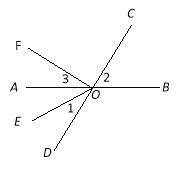
(1)图中∠AOF的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 可得∠BOD= 度;
(3)如果∠1=32°,求∠2和∠3的度数.
参考答案:
【答案】(1)∠BOC、 ∠AOD;(2)对顶角相等; 160°;(3)∠2=64°,∠3=26°
【解析】
试题分析:(1)根据垂直得出∠AOF的余角为∠AOD,然后根据对顶角的性质得出∠BOC;(2)根据对顶角相等的性质得出答案;(3)首先根据角平分线的性质得出∠AOD的度数,然后根据对顶角的性质得出∠2的度数,最后根据垂直的性质得出∠3的度数.
试题解析:(1)∠BOC、 ∠AOD
(2)对顶角相等; 160°
(3)∵OE平分∠AOD ∴∠AOD=2∠1=2×32°=64° ∴∠2=∠AOD=64°
∵OF⊥OC ∴∠DOF=∠COF=90° ∴∠3=90°-∠AOD=90°-64°=26°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的函数y=kx2+k2x﹣2的图象与y轴交于点C,
(1)当k=﹣2时,求图象与x轴的公共点个数;
(2)若图象与x轴有一个交点为A,当△AOC是等腰三角形时,求k的值.
(3)若x≥1时函数y随着x的增大而减小,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab+2ab+a. 如:13=1×3+2×1×3+1=16
(1)求3(﹣1)的值;
(2)若(a+1)2=36,求a的值;
(3)若m=2x,n=(
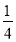 x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校需要置换一批推拉式黑板,经了解,现有甲、乙两厂家报价均为200元/米2,且提供的售后服务完全相同,为了促销,甲厂家表示,每平方米都按七折计费;乙厂家表示,如果黑板总面积不超过20米2,每平方米都按九折计费,超过20米2,那么超出部分每平方米按六折计费.假设学校需要置换的黑板总面积为x米2.
(1)请分别写出甲、乙两厂家收取的总费用y(元)与x(米2)之间的函数关系式;
(2)请你结合函数图象的知识帮助学校在甲、乙两厂家中,选择一家收取总费用较少的.
-
科目: 来源: 题型:
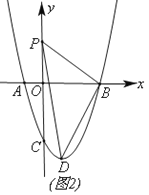
查看答案和解析>>【题目】如图,在平面直角坐标中,抛物线y=ax2-2ax-3a(a≠0)与x轴交于A、B(A在B的左侧),与y轴交于点C,且OC=3OA.
(1)如图(1)求抛物线的解析式;
(2)如图(2)动点P从点O出发,沿y轴正方向以每秒1个单位的速度移动,点D是抛物线顶点,连接PB、PD、BD,设点P运动时间为t(单位:秒),△PBD的面积为S,求S与t的函数关系式;
(3)如图(3)在(2)的条件下,延长BP交抛物线于点Q,过点O作OE⊥BQ,垂足为E,连接CE、CB,若CE=CB,求t值,并求出此时的Q点坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】用双十字相乘法分解因式
例:20x2+9xy-18y2-18x+33y-14。

∵4×6+5×(-3)=9,4×(-7)+5×2=-13,-3×(-7)+2×6=33,
∴20x2+9xy-18y2-18x+33y-14=(4x-3y+2)(5x+6y-7)。
双十字相乘法的理论根据是多项式的乘法,在使用双十字相乘法时,应注意它带有试验性质,很可能需要经过多次试验才能得到正确答案。
分解因式6x2-5xy-6y2-2xz-23yz-20z2=
-
科目: 来源: 题型:
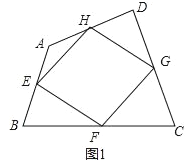
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
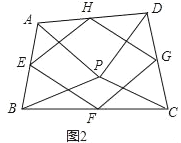
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状,并证明你的猜想.
相关试题

