【题目】已知:关于x的函数y=kx2+k2x﹣2的图象与y轴交于点C,
(1)当k=﹣2时,求图象与x轴的公共点个数;
(2)若图象与x轴有一个交点为A,当△AOC是等腰三角形时,求k的值.
(3)若x≥1时函数y随着x的增大而减小,求k的取值范围.
参考答案:
【答案】(1)图象与x轴公共点只有一个;(2)k的值为﹣1+![]() 或﹣1﹣
或﹣1﹣![]() 或1;(3)﹣2≤k<0.
或1;(3)﹣2≤k<0.
【解析】分析:(1)△=b2-4ac=0时,抛物线与x轴有1个交点(或者把k=-2代入函数关系,直接求得抛物线与x轴的交点横坐标);
(2)根据△AOC是等腰直角三角形易求点A的坐标为(2,0)或(-2,0).把点A的坐标代入函数解析式,通过方程来求k的值;
(3)由“k≥1时函数y随着x的增大而减小”可知,抛物线开口向下.则k<0,且对称轴在直线x=1的左侧,故﹣![]() ≤1,即
≤1,即![]() ≤1.
≤1.
详解:(1)方法一:当k=﹣2时,函数为y=﹣2x2+4x﹣2,
∵b2﹣4ac=42﹣4×(﹣2)×(﹣2)=0.
∴图象与x轴公共点只有一个.
方法二:当k=﹣2时,函数为y=﹣2x2+4x﹣2,
令y=0,则﹣2x2+4x﹣2=0,
解得:x1=x2=1,
∴图象与x轴公共点只有一个;
(2)当△AOC是等腰三角形时,
∵∠AOC=90°,OC=2,
∴可得OA=OC=2.
∴点A的坐标为(2,0)或(﹣2,0).
把x=2,y=0代入解析式 得2k2+4k﹣2=0,
解得 k1=﹣1+![]() ,k1=﹣1﹣
,k1=﹣1﹣![]() ,
,
把x=﹣2,y=0代入解析式 得﹣2k2+4k﹣2=0,
解得 k1=k2=1.
∴k的值为﹣1+![]() 或﹣1﹣
或﹣1﹣![]() 或1;
或1;
(3)由“x≥1时函数y随着x的增大而减小”可知,抛物线开口向下,
∴k<0,且对称轴在直线x=1的左侧,
∴﹣![]() ≤1,即
≤1,即![]() ≤1.
≤1.
解不等式组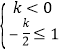 ,
,
解得﹣2≤k<0.
-
科目: 来源: 题型:
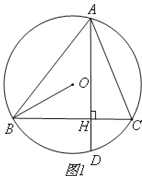
查看答案和解析>>【题目】如图,△ABC内接于⊙O,弦AD⊥BC,垂足为H,连接OB.
(1)如图1,求证:∠DAC=∠ABO;
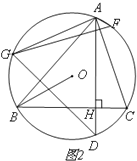
(2)如图2,在弧AC上取点F,使∠CAF=∠BAD,在弧AB取点G,使AG∥OB,若∠BAC=600,
求证:GF=GD;
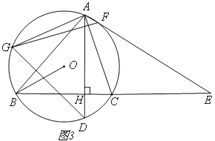
(3)如图3,在(2)的条件下,AF、BC的延长线相交于点E,若AF:FE=1:9,求sin∠ADG的值。
-
科目: 来源: 题型:
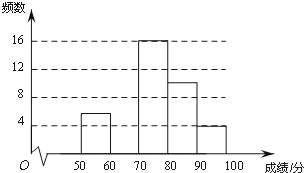
查看答案和解析>>【题目】为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分
频数
频率
50≤x<60
6
0.12
60≤x<70
a
0.28
70≤x<80
16
0.32
80≤x<90
10
0.20
90≤x≤100
c
b
合计
50
1.00
(1)表中的a=______,b=______,c=______;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块Rt△ABC的纸片,∠ABC=900,AB=6,BC=8,将△ABC沿AD折叠,使点B落在AC上的E处,则BD的长为( )
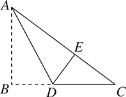
A.3B.4C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab+2ab+a. 如:13=1×3+2×1×3+1=16
(1)求3(﹣1)的值;
(2)若(a+1)2=36,求a的值;
(3)若m=2x,n=(
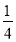 x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校需要置换一批推拉式黑板,经了解,现有甲、乙两厂家报价均为200元/米2,且提供的售后服务完全相同,为了促销,甲厂家表示,每平方米都按七折计费;乙厂家表示,如果黑板总面积不超过20米2,每平方米都按九折计费,超过20米2,那么超出部分每平方米按六折计费.假设学校需要置换的黑板总面积为x米2.
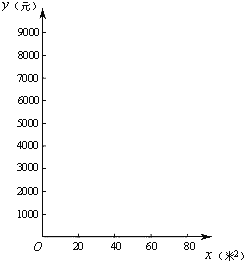
(1)请分别写出甲、乙两厂家收取的总费用y(元)与x(米2)之间的函数关系式;
(2)请你结合函数图象的知识帮助学校在甲、乙两厂家中,选择一家收取总费用较少的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
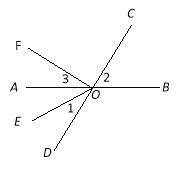
(1)图中∠AOF的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 可得∠BOD= 度;
(3)如果∠1=32°,求∠2和∠3的度数.
相关试题

